리뷰 작성 : 김한결
<이제 막 MARL에 대한 공부를 시작한 터라 잘못된 점이 많을 수 있습니다>
본 논문을 읽기전에 알면 좋은 논문들
1. Trust Region Policy Optimization - Schulman et al. 2015
2. Settling the Variance of Multi-Agent Policy Gradients - Kuba et al. 2021b
3. Trust Region Policy Optimisation in Multi-Agent Reinforcement Learning - Kuba et al. 2021a
0. Preliminary
본 논문을 요약하자면 다음과 같습니다.
1. Constrained Markov Decision Processes (CMDP)에서 정책 업데이트가 될수록 cost가 작아지는 Multi-Agent
Constrained Policy Optimisation(MACPO) 알고리듬을 제안한다. Practical한 버전 MAPPO-Lagrangian을 제안한다.
리뷰를 시작하기전 본 논문은 일종의 TRPO의 MARL 확장버전이다 보니, 잠시 이에 대해 살펴 보겠습니다.
임의의 stochastic policy를 $\pi$라고 했을때 이에 대한 expected discounted reward(간단히 해당 정책의 performance라 생각하시면 됩니다)를 다음과 같이 표현할 수 있습니다.
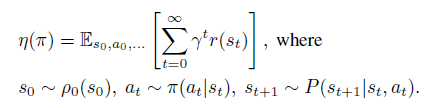
또한 두 임의의 정책 $\pi$와 $\tilde{\pi}$의 성능 차이를 다음과 같이 표현할 수 있습니다.

그래서 $\eta(\pi)$보다 더 좋은 정책을 갖는 $\eta(\tilde{\pi})$는 우변의 $\Sigma_a\tilde{\pi}(a|s)A_{\pi}(s,a)\ge0$ 인 정책 $ \tilde{\pi}$를 찾으면 얻을 수 있습니다. 그런데 문제가 $\tilde{\pi}$는 저희가 찾고자하는 정책이기때문에 해당 정책을 통해 $\mathbb{E}$를 계산할 수 가 없습니다. 그래서 아래와 같은 surrogate func을 통해 policy update를 진행합니다.

그런데 단순히 이를 이용해 update를 해서는 안됩니다. 왜냐하면 1계 미분에서만 $\eta$와 $L$이 같기때문에 policy improve를 보장하기위에서는 무작정 update를 하는 것이 아니라 update의 상한을 두고 해야하죠. 이를 보장하는 bound는 포함하여 다음과 같이 표현할 수 있습니다. (더 자세한 내용은 다음을 참고하세요 URL)

1. Problem Formulation
일반적인 MDP와 달리 constrained Markov game은 $<N,S,\boldsymbol{A},p,\rho^0,\gamma,R,C,c>$으로 구성된 CMDP를 사용합니다. 여기서 $N$은 set of agents, $ \boldsymbol{A} $는 $\Pi^n_{i=1}A^i$인 the product of the agents' action spaces, $C$는 set of cost functions, $c$는 set of cost-constraining values를 의미합니다.
본 논문은 Fully-cooperative setting where all agents share the same reward function을 가정하기에 다음과 같은 목적함수(the expected total reward)를 최대화하는 것이 목표입니다.

반면 각 agent는 다음과 같은 safety constraints를 갖게 됩니다.

여기서 $-Cost=Reward$로 표현하면 복잡한 CMDP가 아닌 MDP로 풀 수 있는 것 아닌가?라는 의문이 들 수 도 있지만 일반적인 MDP와는 차이를 둬야하는 이유는 constraint때문입니다. (해당 문제를 $Reward-Cost$로 변형하여 MDP로 풀게되면 constraint 상한과 관계없이 $Reward-Cost$가 아주 높은 나오는 정책이 나올 수 있기때문)
해당 수식 다음 문단에는 다음과 같은 문장이 나오는데 . Although the action $a^i_t$ of agent i does not directly influence the costs ${C^k_j(s_t; a^k_t)}^{m^k}_{j=1}$ of other agents $k \ne i$, the action $a^i_t$ will implicitly influence their total costs due to the dependence on the next state 이는 cost function의 input이 $s_t, a_t$뿐이지만 expection의 Subscript notation이 $\mathbf{\pi}$인 이유를 설명합니다.
해당 논문에서는 각 agent가 공통된 보상함수를 쓰기 때문에 state-action value function와 the state-value function을 다음과 같이 정의할 수 있습니다.

그리고 다음 단락에는 각 agent마다 별도의 cost function을 다음과 같이 정의합니다.

여기서 $-i$는 i 여집합을 의미하는 complement 입니다. 위 식을 말로 풀어서 하자면 i번째의 agent는 $s$와 $a^i$로 정해져있고 그 이위의 complement들을 sampling 해서 얻은(정확히는 sampling이라고 할 수 없지만) cumulative discount cost가 $Q^i_{j,\pi}(s,a^i)$의 정의가 됩니다.
(여기서부터 action-value function과 Advantage에 대한 내용은 Kuba et al. 2021a, Kuba et al. 2021b에서 처음으로 정의된게 많으므로 이를 참고하시길 바랍니다)
해당 논문에서는 다음과 같은 multi-agent state-action value function을 정의합니다. 여기서 $a$는 정해진 값, $\mathrm{a}$는 확률변수라 생각하시면 편합니다.

위와 같이 state-action value function을 정의한 이유는 다음과 같이 multi-agent advantage function을 정의하기 위해서 입니다. 여기서 유의해야할 점이 $j_{1:k}$와 $i_{1:m}$는 disjoint이고 $a^{j_{1:k}}$와 $a^{i_{1:h}}$는 정해진 값입니다. (저는 위 notation이란 헷갈려서,,)

또한 multi-agent advantage function을 위와 같이 정의하면 다음과 같은 Lemma를 얻을 수 있습니다.

위 Lemma의 증명은 Appendix에서 확인할 수 있습니다.

위 증명은 Kuba et al. 2021b의 Appendix에서 더 자세하게 확인할 수 있습니다.

2. Multi-Agent Constrained Policy Optimisation
Kuba et al. 2021a에서는 위 Lemma를 이용하여 다음과 같은 surrogate return을 정의함으로써 multi-agent trust region method를 제안합니다. 여기서 $ \hat{\pi}^{i_{h}} $는 임의의 정책을 의미합니다. TRPO의 surrogate return과는 다소 차이가 있는 이유는 TRPO에서의 surrogate function는 $L_{\pi}(\tilde{\pi}) = \eta(\pi) + \Sigma_{s}\rho_{\pi}(s) \Sigma_{a}\tilde{\pi}(a|s)A_{\pi}(s,a)$로 정책 $\pi$의 performance에 Advantage를 더했지만 multi-agent surrogate return에서는 $\hat{\pi}^{i_h}$에 대한 advantqage function만을 의미합니다. 또한 이러한 정의는
surrogate $ L_{\pi}^{i_{1:h}}(\bar{\mathbf{\pi}}^{i_{1:h-1}},\bar{\pi}^{i_h}) $의 합을 이용해 joint surrogate return을 다음과 같이 정의할 수 있도록 만들어 줍니다.

따라서 다음과 같은 optimisation problem을 풀면서 joint surrogate return $L_{\pi}$를 키울 수 있습니다. ( $ L_{\pi}^{i_{1:h}}(\bar{\mathbf{\pi}}^{i_{1:h-1}},\bar{\pi}^{i_h}) $ 의 합이 $L_{\pi}$가 되므로 각 $ L_{\pi}^{i_{1:h}}(\bar{\mathbf{\pi}}^{i_{1:h-1}},\bar{\pi}^{i_h}) $가 모두 커지다면 $L_{\pi}$가 커진다고 할 수 있음) (아래 식은 TRPO 식(9)번을 참고하세요 )


또한 i번째 agent가 가지고 있는 j번째 cost에 대해 다음과 같은 부등식을 만족합니다. 여기서 reward가 아닌 cost로 정의했기 때문에 새로운 정책 $J^i_j(\bar{\pi})$는 TRPO에서 봤던 부등식에 의해 $J^i_j(\pi)$보다 작거나 같아야합니다. 대부분은 TRPO와 유사하지만 "Notice now that..." 부분과 jensen's inequality가 필요한 부분만 조금 다릅니다.


이제 위 Lemma 4.3을 만족하도록 constraint를 걸어주고 update를 Multi-agent TRPO와 함께 해주면 됩니다. (본 논문의 4.2절에는 contraint를 primal-dual optimisation으로 변형하는 방법이 나오는데 제가 linear quadratic optimisation problem이 기억이 가물가물해서 해당 포스터에서는 일단 넘어가도록 하겠습니다)
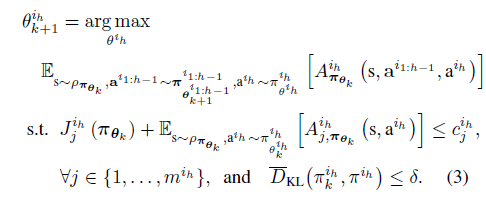


여기서 $A^{i_h,(\lambda)}_{\pi_{\theta_k}}$는 다음과 같이 정의하고
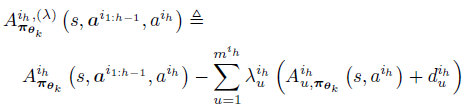
또한 MACPO optimisation problem을 linear quadratic constraint로 푸는게 아니라 lagrangian만 정리하면

이때 hessian이 필요한 constraint를 수학적으로 풀어낸것이 아닌 적당히 괜찮은 값 $\epsilon$으로 대체하여 update하면 다음과 같이 쓸 수 있습니다.

3. Experiment result

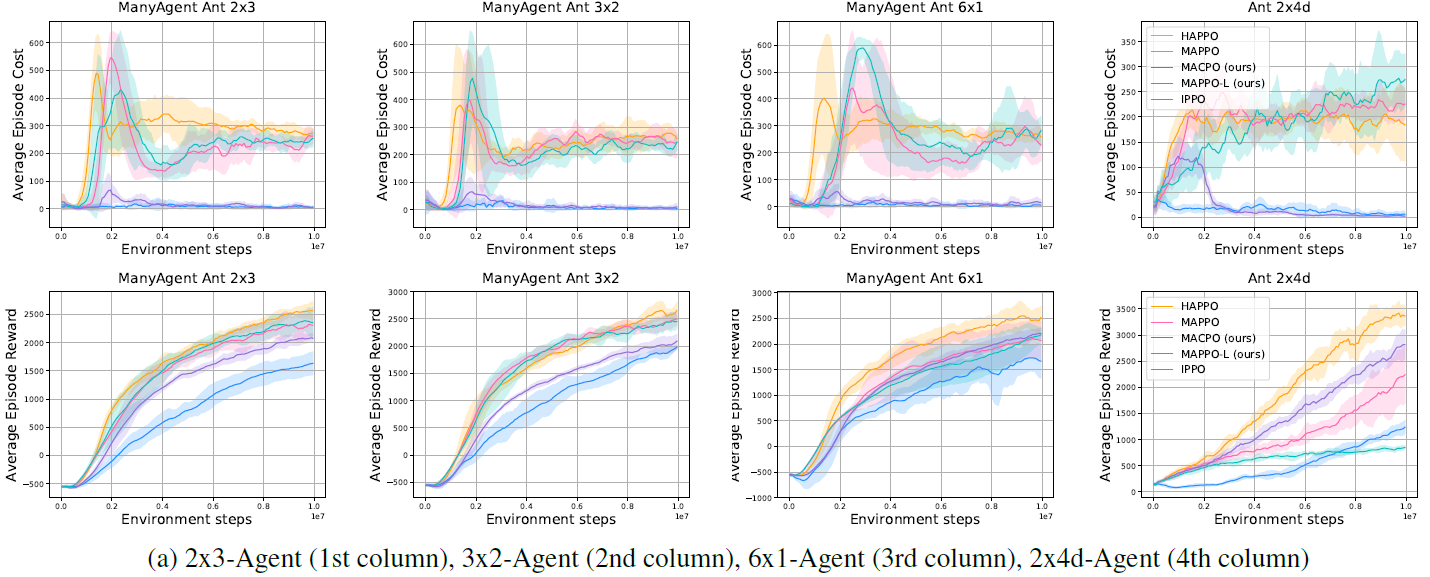



'Paper Review' 카테고리의 다른 글
| Language Guided Skill Discovery(LGSD) 리뷰 (4) | 2024.11.12 |
|---|---|
| Adversarial Intrinsic Motivation for Reinforcement Learning (2021) 논문 리뷰 (4) | 2024.08.14 |
| Planning with Goal-Conditioned Policies (2019) 논문 리뷰 (4) | 2023.05.14 |
| Reference Learning and Control as Probabilistic Inference: Tutorial and Review 논문 리뷰 (4) | 2022.06.12 |
| Variational Adversarial Imitation Learning (VAIL) 논문리뷰 (2) | 2022.02.26 |



