리뷰 작성: 김장원 (jangwonkim@postech.ac.kr)
1. Introduction
최근의 강화학습은 바둑, 아타리 게임, 로봇의 locomotion 등 다양한 환경에서 성공적으로 동작할 수 있음을 보였다. 그러나 보상이 희소한 환경에서는 에이전트 학습이 까다로울 수 있다. 이러한 환경에서 유의미한 학습을 하기 위해서는 더 많고 효율적인 탐험이 필요하다.
보상이 희소한 환경에서 에이전트의 학습 속도를 높이기 위한 여러 연구들이 진행되었다. 희소한 보상 함수를 수정하여 dense하게 만들거나 (reward shaping), 내재적 보상 (intrinsic reward)를 부여하는 것을 예로 들 수 있다. 이 논문 역시 일종의 내재적 보상을 활용하여 희소 보상 환경에서 에이전트를 학습시킨다. 이 때 사용하는 내재적 보상은 에이전트의 상태 방문 분포 (state visitation distributio -n)과 타겟 분포 (target distribution)과의 mismatch의 정도로 표현한다. 정확히는 이 두 분포의 Wasserstein-1 거리가 최소가 되도록 내재적 보상이 부여된다. 이렇게 재 정의된 보상을 최대화하는 알고리즘이 이 논문에서 제안한 Adversarial Intrinsic Motivation (AIM) 이다.
일반적으로 머신러닝에서 거리 (metric)은 보통 유클리디안 거리를 많이 사용한다. 그러나 때때로 유클리디안 거리는 강화학습 task에 적합하지 않은 경우가 존재한다 (미로 찾기 등). 따라서 본 논문에서 저자는 time-step metric이라는 특별한 quasimetric (대칭성을 보장하지 않는 metric)을 제안한다.
추후에 살펴보겠지만, 이 time-step quasimetric을 사용하여 Wasserstein-1 distance를 최소화하는 것은 에이전트가 goal 상태에 도달하는 데 걸리는 time-step의 기댓값을 최소화하도록 정책을 학습하는 것과 같다. 특히 결정론적 환경에서는 이 정책이 최적 정책임이 보장된다. 아울러 AIM은 확률론적 환경에서도 잘 동작함을 실험적으로 보여주었고, 또한 Hindsight Experience Replay (HER) 알고리즘과 결합하여 사용하였을 때, 에이전트의 학습 속도가 높은 폭으로 향상되었음을 보였다.
2. Related Work
2.1. Intrinsic Motivation
내재적 동기 (Intrinsic Motivation)은 외부 task-specific reward에 추가되는 보상 (내재적 보상)을 의미한다. 내재적 동기를 이용한 알고리즘은 RL 문헌에서 많이 연구가 되었고, 실제로 탐험을 장려하는 좋은 수단이 될 수 있음을 보였다. 본 논문에서 내재적 보상으로 사용하는 Wasserstein 거리에 대한 활용 및 연구 역시 imitation learning 등에서 진행되고 있다.
2.2. Goal-Conditioned Reinforcement Learning
https://rlwithme.tistory.com/19 참고
2.3. Adversarial Imitation Learning and Minimizing Distribution Mismatch
Adversarial imitation learning은 에이전트의 state-action visitation 분포와 전문가의 trajectories 분포 간의 mismatch를 줄이는데 효과적인 방법임이 입증되었다. 그 유명한 Generative Adversarial Imitation Learning (GAIL) 알고리즘의 Adversarial imitation learning의 대표적인 예이다. 대부분의 경우 전문가 trajectories 분포는 실현 가능하며, 따라서 에이전트의 state-action visitation 분포와 이 trajectories 분포를 정확히 맞추는 데 초점을 맞춘다. 그러나 본 논문의 경우, 실현 불가능한 target 분포와 state-action visitation 분포의 거리를 최소화 하는 것에 초점을 둔다.
3. Background
3.1. Goal-Conditioned Reinforcement Learning
GCRL 서베이 참고.
3.2 Optimal Transport and Wasserstein-1 Distance
Optimal transport 이론은 하나의 분포를 다른 분포로 ‘옮기는’ 데 얼마나 많은 ‘일’ (work)이 필요한 지를 다루는 이론이다. 여기서 ‘일’이란 ground metric $d$로 정의된다. 좀 더 구체적으로 거리 공간 (metric space) $\mathcal{(M,d)}$ 이 있다고 하자. ($\mathcal{M}$은 집합이고 $d$는 $\mathcal{M}$상의 거리 (metric) 이다.) 이 때 두 분포 $\mu, \nu$ 의 Wasserstein-p 거리는 다음과 같다:

여기서 $Z$는 모든 가능한 couplings (각각의 marginals로 $\mu$와 $\nu$를 가지는 결합 분포 $\zeta\in\Delta(\mathcal{M}\times \mathcal{M})$) 을 원소로 가지는 집합이다. Optimal coupling을 찾는 다는 것은 일의 척도 $d$를 사용하였을 때, 최소한의 일을 통해 분포 $\mu$를 분포 $\nu$로 옮기는 방법을 찾는 것을 의미한다. 이 Wasserstein-p는 종종 RL에이전트가 주어진 target 분포를 맞추기 위한 보상 (음수)으로 사용되기도 한다.
식 (1)을 활용하여 Wasserstein 거리를 찾는 것은 쉽지 않다. 따라서 머신러닝 분야에서는 종종 Wasserstein-1 거리를 추정하고자 할 때, 포텐셜 함수를 활용하는 강력한 dual form인 Kantorovich-Rubinstein duality를 이용한다. Wasserstein-1 거리의 Kantorovich-Rubinstein duality는 아래와 같다:

또한 최근에 밝혀진 연구에 따르면, 다행히 이 dual form은 quasimetric 공간으로 확장될 수 있다 (Jevtic, 2018).
4. Time-Step Metric
Wasserstein-1 거리를 사용할 때 ground metric $d$를 무엇으로 정해야 할까? 유클리디안 거리는 상당히 매력적인 선택지로 보이지만, 몇몇 task에 대해서는 적절하지 않을 수 있다. 아래 그림과 같은 task를 생각해보자.
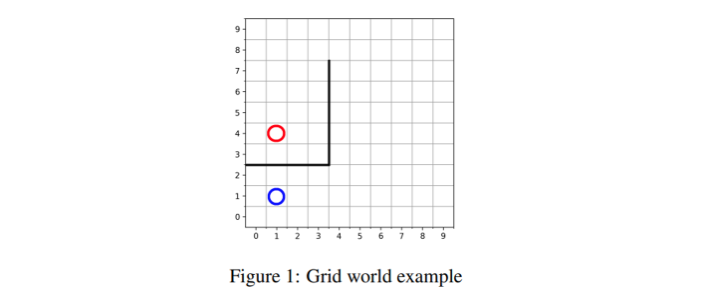
이 task에는 통과할 수 없는 벽 (bold line)이 존재한다. 만약 Manhattan 거리를 d로 사용한다면, 빨간색 상태와 파란색 상태가 벽이 존재하더라도 가깝기만 하면 거리가 작은 상태로 생각할 것이다. 이는 적절하지 않다. 따라서 저자들은 time-step metric이라는 새로운 d를 정의한다.

Time-step metric $d^{\pi}_{T}(s,s_g)$은 현재 상태 ($s$)에서 에이전트가 주어진 정책 ($\pi$)을 따를 때, 목표 상태 ($s_g$)까지 도달하는 데 걸리는 평균 time-step을 의미한다. Time-step metric은 대칭이 보장되지 않으므로 quasimetric 이다.
Time-step metric은 goal에 도착하는 경우를 제외하고는 transition 한번 당 1만큼 비용이 커지므로, 다음과 같이 재귀적으로 표현이 가능하다:

한편 Wasserstein-1 거리의 duality를 살펴보면 포텐셜 함수의 립시츠 상수가 1이라는 제한이 있다. 포텐셜 함수의 립시츠 상수 \text{Lip}(f)는 아래 식과 같이 표현될 수 있다.
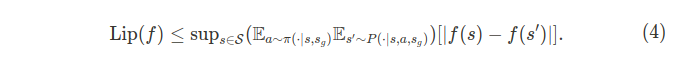
포텐셜 함수의 립시츠 상수가 1이라는 제한을 만족시키기 위해 clipping, gradient penalty, 그리고 spectral normalizing 등의 다양한 기법들이 존재한다.
이제 이 time-step 거리와 goal-conditioned RL의 가치 함수 간의 연관을 생각해보자. 만약 외부 리워드가 goal 상태에 도달했을 때를 제외하고 다 0이라면, 가치 함수는 $V^{\pi}(s|s_g)=\mathbb{E}[\gamma^{T(s_g|\pi,s)}]$ 와 같다. 따라서 가치 함수와 time-step metric $d^{\pi}_T(s_0,s_g)$와는 아래와 같은 관계를 가진다.

증명은 Jensen’s inequality를 이용하면 간단히 보일 수 있으며, 따로 기술하지는 않겠다.
아울러 Jensen gap $\Delta^{\pi}_{Jenson}(s):=V^{\pi}(s|s_g)-\gamma^{d^{\pi}_T(s,s_g)}$ 는 오직 $\text{Var}(T(s_g|\pi,s))=0$일 때만 0이 된다 (Liao and Berg, 2018). 따라서 다음을 주장할 수 있다.

5. Wasserstein-1 Distance for Goal-Conditioned Reinforcement Learning
이 장에서는 본격적으로 goal-conditioned RL 문제와 Wasserstein-1 거리를 연관짓는다. 5.1.장에서는 time-step metric $d^{\pi}_T$을 척도로 가지는 Wassersten-1 거리에 대한 분석을 진행하며, 5.2.장에서는 Kantorovich-Rubinstein 듀얼리티를 이용한 내재적 보상함수를 설계한다.

다음 proposition은 Jenson gap과 이 Wasserstein-1 거리의 관계를 보여준다.
Proposition 3. For a given policy \pi, the Wasserstein distance of the state visitation measure of that policy from the goal state distribution \rho_g under the ground metric d^{\pi}_T can be written as
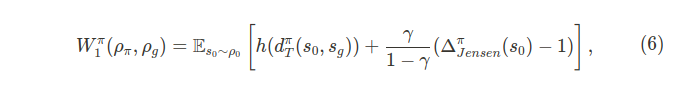
where h is an increasing function of d^{\pi}_T.
여기서 \Delta^{\pi}_{Jensen}=\mathbb{E}[\gamma^{T(s_0)}|s_0]-\gamma^{d^{\pi}_{T}(s_0,s_g)}이다. Proposition 3에서 확인할 수 있는 부분은 첫 번째로 Wasserstein 거리는 타입 스텝 수의 기댓값에 의존한다는 점이다. Wasserstein 거리는 타임 스텝의 수가 줄어듬에 따라 같이 줄어든다. 두 번째는 Wasserstein 거리가 risk-averse한 성질을 보인다는 것이다. 구체적으로 Jensen gap의 바운드는 음수가 아닌 두 상수 C_1,C_2에 의해 정해진다. 즉,

위 식에서 우리는 타입 스텝의 분산이 작을 수록 Jensen gap이 줄어듬을 확인할 수 있다. 이는 결국 Wasserstein 거리가 줄어드는 효과를 보여준다. 또한 환경이 결정론적이라면 Goal-conditioned RL에서의 최적 정책과 Wasserstein distance의 관계는 아래와 같다.

환경이 결정론적이라면 Jensen gap이 사라짐을 Proposition 2.에서 보였다. 또한 식 (6)에서 Jensen gap이 사라진다면, Wasserstein 거리는 initial state s_0에서 expected distance가 늘어남에 따라 단조 증가하게 된다. 따라서 이 expected distance를 최소화 하는 정책이 당연히 최적 정책일 것이다.
5.2. Adversarial Intrinsic Motivation to minimize Wasserstein-1 Distance
Wasserstein 거리를 최소화 하는 정책이 goal-conditioned RL 에서의 최적 정책임을 보였으니, 이제 이 Wasserstein 거리를 최소화하는 방법에 대해 생각해보자. 우리가 식 (2)의 dual-form을 사용하면 ground metric $d^{\pi}_T$를 계산하지 않더라도 Wasserstein 거리를 최소화 할 수 있음을 확인하였다. 따라서 이 duality를 활용하여 Wasserstein를 최소화하는 작전을 세워보자.
Goal-conditioned 정책의 파리미터를 $\theta \in \Theta$라 하고, 이 정책을 통해 생성되는 state-visitation 분포를 $\rho_{\theta}$라고 하자. 그러면 우리는 $\rho_{\theta}$와 주어진 $s_g$ 에 대한 goal-conditioned target 분포 $\rho_g(=\delta(s_g))$의 Wasserstein-1 거리를 최소화해야한다. 파라미터 $\phi$로 매개화되어 있는 포텐셜 함수 $f_{\phi}:\mathcal{S}\times \mathcal{S} \to \mathbb{R}$를 사용한다면, 이 포텐셜 함수와 에이전트는 아래와 같이 adversarial objective를 가진다.

그런데 포텐셜 함수 f_{\phi}는 립시츠 상수가 1이여야 하는 제한 조건이 있기 때문에, 식 (4)와 식 (7)을 결합하여 포텐셜 함수에 대한 objective를 다음과 같이 세울 수 있다.
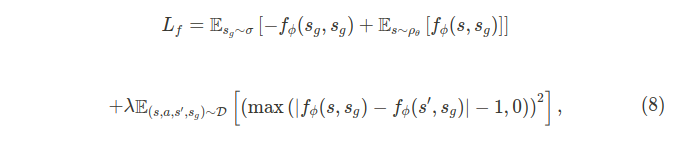
여기서 $\mathcal{D}$는 이상적으로는 모든 상태와 expected goal을 포함하고 있는 분포이다. 이것은 보통 불가능하기 때문에 AIM은 replay buffer를 이용하여 $\mathcal{D}$를 근사한다. 그리고 HER와 비슷하게 각 에피소드 마다 도착한 상태를 achieved goal로 relabel한다.
이제 내재적 보상을 설계해보자. 저자들은 직접적으로 Wasserstein 거리를 줄이도록 아래와 같이 내재적 보상을 설계하였다.

또한 저자들은 위 보상의 두번째 항인 f_{\phi}(s_g,s_g)을 직접적으로 사용하기 보다는 학습의 안정성을 위해 상수 bias를 사용하였다. 보통 어떤 상수를 사용하여도 실험적으로 좋은 결과를 보여주었다. 저자들은 최종적으로 이 bias 상수 b를 \hat{r}의 분산을 줄이기 위해 \text{max}_{s\in \mathcal{S}}f_{\phi}(s',s_g)로 설정하여 실험을 진행하였다. 즉 최종적인 내재적 보상은 다음과 같다.
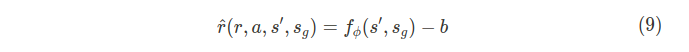
이 내재적 보상을 사용하여 학습을 하는 AIM과 HER를 결합한 알고리즘의 의사 코드는 다음과 같다.

6. Experiments
저자들이 제안한 AIM은 실험을 통해 다음 4가지를 보였다.
- AIM은 희소 보상 환경에서 단일 목표를 달성하기 위한 정책을 빠르게 학습하도록 도와준다.
- 학습된 내재적 보상이 에이전트가 목표를 달성하는데 좋은 퀄리티로 가이드를 해주는가?
- AIM이 확률론적 전이를 가지는 환경이나 state feature의 sharp changes가 발생하는 환경에서도 잘 동작하는가?
- 연속적인 상태, 행동 공간을 가지는 환경에서도 AIM이 잘 동작하는가?
다음은 그리드 환경에서 AIM이 학습된 내재적 보상의 분포를 보여준다.

학습이 될 수록 보상이 잘 설계 됨을 (b)에서 확인할 수 있다. 또한 AIM 보상을 사용하였을 때 state-vistitation 이 우리가 원하는 방향으로 분포됨을 확인할 수 있다 (a). 하지만 희소 보상환경에서 주어지는 보상만을 사용하였을 때는 정책이 잘 학습되지 않는 것을 확인할 수 있다 (c). 다음은 연속적인 상태, 행동 공간을 가지는 Fetch Robot 환경에서의 결과이다.

여기서 L2+HER 베이스라인은 goal state와 현재 state의 유클리디안 거리를 보상으로 사용하였다. 이는 일종의 oracle과 같은 보상 함수이며, AIM+HER가 얼마나 잘 동작하는지 알 수 있는 척도로 사용될 수 있다.
7. Summary
본 논문은 희소 보상 환경에서 에이전트가 잘 학습할 수 있도록 내재적 보상을 도입한 알고리즘인 AIM을 제안한다. AIM에서 사용하는 내재적 보상은 에이전트의 state-visitation 분포와 목표 타겟 분포 (디락 분포로 표현되는) 간의 Wasserstein-1 거리를 작게 만드는 방향으로 설계된다.
본 알고리즘의 정당화를 위해 저자들은 time-step metric이라는 quasimetric 공간을 제안하였고, 이를 ground metric으로 가지는 Wasserstein-1 거리를 가장 작게 만드는 goal-conditioned 정책이 최적 정책임을 보였다.
'Paper Review' 카테고리의 다른 글
| Language Guided Skill Discovery(LGSD) 리뷰 (4) | 2024.11.12 |
|---|---|
| Multi-Agent Constrained Policy Optimisation(MACPO, MAPPO-Lagrangian) 논문리뷰 (4) | 2024.02.19 |
| Planning with Goal-Conditioned Policies (2019) 논문 리뷰 (4) | 2023.05.14 |
| Reference Learning and Control as Probabilistic Inference: Tutorial and Review 논문 리뷰 (4) | 2022.06.12 |
| Variational Adversarial Imitation Learning (VAIL) 논문리뷰 (2) | 2022.02.26 |



