리뷰 작성: 김장원 / 석사과정 (jangwonkim@postech.ac.kr)
0. Abstract
본 논문에서는 반복적 절차(Iterative Procedure)를 통한 정책 향상 알고리즘을 소개하고 있습니다. TRPO라고 불리는 이 알고리즘은 이론적으로 정책향상을 보장하는 알고리즘을 실용적으로 적용 가능하게 근사한 것입니다. 이 알고리즘은 신경망과 같이 비선형 정책을 최적화하는데 효과적인 Natural Policy Gradient 방법과 비슷합니다. TRPO는 robotic swimming, hopping 등과 같은 다양한 Task에서 좋은 성능을 보이며 연속적인 행동 공간 제어와 관련해서 Policy Gradient의 가능성을 보여준 알고리즘입니다. 또한 TRPO는 연속적인 행동 공간뿐만 아니라 이산적인 행동 공간 환경에서도 사용이 가능합니다.
TRPO는 Trust Region Policy Optimization의 약자로, 정책에 의해 행동해야 할 행동이 확률적으로 표현되는 ‘‘확률론적 정책'‘의 향상을 보장하기 위해 Trust Region이라는 개념을 도입하였기에 이러한 이름이 붙여졌습니다. TRPO는 on-policy 알고리즘이기에 local-optima에 빠질 위험이 존재합니다. 그러나 local-optima에 빠질지언정 이론적으로 정책 향상이 보장되는 장점을 가지고 있습니다. TRPO의 또다 른 장점은 타 알고리즘에 비해 비교적 하이퍼-파라미터의 수가 적어 다양한 환경에서의 튜닝에 의한 노력이 크게 준다는 점입니다. 이는 TRPO가 상당히 일반화된 알고리즘임을 말하기도 합니다.
1. Introdiction
최적 정책을 찾는 방법은 크게 3가지 카테고리로 묶을 수 있습니다.
- 정책 반복 방법 (Policy Iteration Methods)
- 현재 정책상에서 가치 함수를 평가하고, 이를 바탕으로 정책을 향상시키는 것을 반복하는 방법
- 정책 경사도 방법 (Policy Gradient Methods)
- 샘플 궤적(Sample Trajectories) 하에 얻은 보상의 합의 기댓값의 기울기를 추정량으로 하여 정책을 학습하는 방법
- 본 논문에서는 이후 정책 경사도 방법과 정책 반복 방법과의 연결점을 이야기하고 있습니다.
- Derivative-free 최적화 방법
- Cross-Entropy Method(CEM)이나 Covariance Matrix Adaptation(CMA) Method와 같이 보상의 합을 black box 함수로 두고 정책을 향상시키는 방법
본 논문의 TRPO는 정책 경사도 방법을 이용한 알고리즘입니다. 정책 경사도 방법은 경사도를 이용하여 보상의 합(object function)을 증가시키는 방향으로 정책을 향상시키는데, first-order 경사도를 이용한다면, 곡선이 있는 영역에서 부정확할 수 밖에 없습니다. 예를 들어 경사도 정책에서의 step-size(경사도를 바탕으로 얼마나 많이 갱신할지의 지표) 가 크다면, 과장된 정책 향상의 방향을 그대로 믿고 정책 업데이트를 할 수도 있게 됩니다. 이렇게 되면 정책 향상이 올바르게 수렴하지 않을 가능성이 있습니다. 그렇다고 step-size를 너무 작게하면 학습의 속도가 너무 느려진다는 단점이 있습니다.
앞으로 자세히 살펴보겠지만 TRPO는 이론적인 알고리즘을 실용적으로 사용하기 위해 근사한 알고리즘입니다. 이 근사 된 알고리즘이 잘 통하기 위해서는 정책 갱신의 step-size가 충분이 작아야 합니다. 그렇다면 이 step-size가 얼마나 작아야할까요? 무턱대고 step-size를 매우 줄이면 학습 효율이 매우 떨어질 겁니다.
요약하자면 본 논문은,
- 먼저 정책 향상이 보장되는 이론적인 알고리즘을 제시합니다.
- 이 이론적인 알고리즘을 실용적으로 적용하기 위해 근사합니다.
- 이렇게 근사 된 알고리즘을 통해 정책을 최적 정책으로 수렴시키고 싶습니다.
- 그러나 갱신을 할 때 step-size가 너무 크면 정책이 잘 수렴하지 않습니다.
- step-size가 너무 크면 이론적인 알고리즘을 실용적인 알고리즘으로 근사할 수 없기 때문입니다.
- 따라서 step-size의 크기에 대한 영향을 분석하고, 이에 따라 크기를 제한해야 합니다.
따라서 본 논문에서는 TRPO로 불리는 step-size의 크기를 제한하면서, 정책 향상이 보장된 근사된 알고리즘을 제안합니다.
2. Preliminaries
1. 할인이 포함된 MDP는 다음과 같이 정의 됩니다.

2. 할인된 누적 보상의 기댓값(Expected Discounted Reward)
현재 정책이 $\pi$이고, 초기 상태를 $s_{0}$라고 한다면 이 정책을 따랐을 때 예상되는 보상의 합은 다음의 수식과 같습니다.

3. 행동가치 함수(state-action value function) $Q_{\pi}$, 가치 함수(value function) $V_{\pi}$, 그리고 Advantage function $A_{\pi}$ 은 다음과 같이 표현할 수 있습니다.

4. 서로 다른 두 정책하에 얻어지는 리턴(Return)값의 관계
서로 다른 두 정책하에 얻어지는 리턴의 기댓값은 다음과 같은 관계가 있습니다.

표기법 $\mathbb{E}_{s_{0},a_{0},...\ \sim \widetilde{\pi}}[...]$은 $a_{t}\sim \widetilde{\pi}(\cdot |s_{t})$로 샘플된 행동들을 의미합니다. 위 식을 풀어 말하면,
"A라는 정책 하에서 얻어지는 리턴의 기댓값은, 1) B라는 정책 하에서 얻어지는 리턴의 기댓값과, 2) A 정책에서 얻어지는 상태-행동 trajectory에 대한 정책 B하의 Advantage 값을 할인해서 더한 값의 평균을 더한 값이다."
라고 말할 수 있겠습니다.
식(1)의 증명은 다음과 같습니다.

4. (unnormalized) discounted visitation frequencies
discounted visitation frequency란 한 상태를 방문할 할인된 확률의 합으로 정의 됩니다. 즉, $p_{\pi}$ 를 discounted visitation frequency라고 한다면 다음과 같습니다.

여기서 $s_{0}\sim p_{0}$이고, 행동들은 정책 $\pi$를 따라 선택됩니다.discounted visitation frequency란 한 상태를 방문할 할인된 확률의 합으로 정의 됩니다.
이제 식 (1)을 visitation frequency를 이용하여 다음과 같이 전개해나갈 수 있습니다.
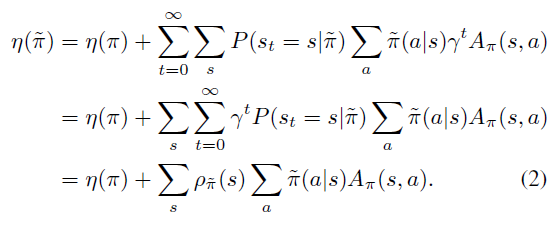
이렇게 얻은 식(2)는 다음과 같은 의미를 내포하고 있습니다.
"만약 모든 상태 s 에 대해서 advantage의 기댓값이 0 이상이라면, $\pi\to \widetilde{\pi}$로의 정책 갱신은 policy performance $\eta$를 증가시킴이 보장된다."
즉, $\sum_{a}^{}\widetilde{\pi}(a|s)A_{\pi}(s,a)\ge 0$ 라면, policy performance $\eta$를 증가시킴이 보장된다고 말할 수 있습니다.
다시 말해, $\sum_{a}^{}\widetilde{\pi}(a|s)A_{\pi}(s,a)\ge 0$ 를 만족하는 정책 $\widetilde{\pi}$를 찾으면 $\eta$를 증가시킬 수 있다는 것입니다. 따라서 $\sum_{a}^{}\widetilde{\pi}(a|s)A_{\pi}(s,a)\ge 0$를 만족하는 $\widetilde{\pi}$로 기존 정책을 갱신해야한다는 갱신의 방향성을 알 수 있습니다.
그러한 정책 중 만약 $\widetilde{\pi}$를 $\widetilde{\pi}(s)=argmax_{a}A_{\pi}(s,a)$로 정한다면 항상 $argmax_{a}A_{\pi}(s,a)\ge 0$를 만족할 것이고, 따라서 정책향상이 항상 보장될 것입니다.
이는 일반적인 deterministic policy로 $\widetilde{\pi}(s)=argmax_{a}A_{\pi}(s,a)$를 사용하는 policy iteration방법과 매우 유사합니다. 이 유사성이 본 논문의 저자들이 말하는 policy iteration method와 policy gradient method의 연결이 될 수 있습니다. 그러나 우리가 추정과 근사의 과정속에 발생하는 에러들로 인해 가끔 $\sum_{a}^{}\widetilde{\pi}(a|s)A_{\pi}(s,a)<0$이 되는 상태가 생길 수 있으며, 이는 보통 불가피합니다.
이제 다시 식
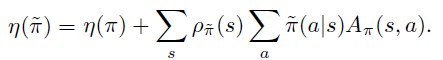
을 보면 $\rho_{\widetilde{\pi}}(s)$부분을 추정하는 것은 상당히 복잡합니다. 왜냐하면 보통 이전 정책으로부터 샘플링을 하고 이 샘플들을 바탕으로 정책경사도를 구하는데, $\rho_{\widetilde{\pi}}(s)$은 갱신할 정책의 visitation frequency이기 때문입니다. 따라서 $\rho_{\widetilde{\pi}}(s)$대신 이전 정책 $\rho_{\pi}(s)$을 사용하여 퍼포먼스를 계산하는 근사 식을 사용하는 것이 편리합니다. 따라서 본 논문에서는 다음과 같은 local approximation을 사용합니다. 직관적으로 매우 짧은 step-size라면, $\rho_{\widetilde{\pi}}(s)$와 $\rho_{\pi}(s)$에서의 변화량은 크지 않을 것이며 따라서 근사식이 가능할 것이라고 생각할 수 있습니다.

식(3)을 보면, $L_{\pi}$는 갱신된 정책 $\rho_{\widetilde{\pi}}(s)$대신 샘플링이 가능한 이전 정책 $\rho_{\pi}(s)$ 사용했습니다. 다시 말해 정책의 변화로 인한 state visitation density의 변화를 무시하였습니다. 이렇게 할 수 있는 이유는 다음과 같습니다. policy로 parameterized policy $\pi_{\theta}$를 사용하고 $\pi_{\theta}(a|s)$가 미분 가능하다면, $L_{\pi}$는 $\eta$와 일차 근사가 일치하기 때문입니다. 이는 다음이 성립한다는 말과 같습니다. (Kakade & Langfold, 2002)

아래는 https://rll.berkeley.edu/deeprlcourse/docs/lec5.pdf에서 발췌한 식 (4)에 대한 설명이 있는 슬라이드 입니다.

식 (4)는 $L_{\pi_{\theta_{old}}}$을 증가시키는 $\pi_{\theta_{0}}\to \widetilde{\pi}$로의 정책 갱신의 step-size를 충분히 작게 하면 $\eta$역시 증가함을 뜻합니니다. 다시 말해 $\pi_{\theta_{0}}$$\to$$\widetilde{\pi}$ 의 변화가 매우 작은 step동안은 $L_{\pi_{\theta_{old}}}$와 $\eta$의 증가 폭이 같습니다. 이는 step-size를 충분히 작게하면 근사가 성립하며 정책 향상이 보장됨을 의미합니다. 그러나 식(4)는 이 근사가 성립하기 위해 step-size를 얼마나 적당히 작게해야하는지에 대한 가이드라인은 제공하고 있지 않습니다. (물론 작을 수록 두 근사가 더 가까워지는 것은 명확하지만, 학습 속도가 떨어지는 단점이 있습니다.)
Conservative Policy Iteration
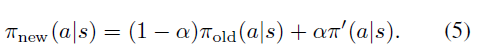
한편 식(5)와 정책을 갱신해 나간다면, step이 작기 때문에 상대적으로 안정적으로 수렴할 수 있게 됩니다.Kakade & Langford는 이렇게 새로운 정책을 현재 정책과 $\pi^{'}$의 mixture로 표현한다면, 새로운 정책의 퍼포먼스는 다음과 같은 lower bound를 가짐을 보였습니다.
- 알파가 0이면 새로운 정책은 이전 정책과 같아지게 되고(성능의 갱신은 없다.), 알파가 1일 때, 성능 향상이 보장되려면 $\pi^{'}$는 모든 상태에서 더 좋은 행동을 선택해야합니다.
- KaKade & Langford는 이러한 문제를 해결하기 위해 conservative policy iteration 이라는 정책 향상 방법을 제안하였습니다. 보수적인 정책 반복이라는 뜻을 가진 이 방법은 정책을 업데이트할 때, 새로운 정책을 $\pi^{'}=argmax_{\pi^{'}}L_{\pi_{old}}(\pi^{'})$으로 바로 사용하는 것이 아니라, 기존 정책과 $\pi^{'}$의 적절한 비율로 나타내는 방법입니다. 따라서 정책의 갱신을 보수적으로(알파 값이라는 비율을 도입하면서 step-size를 줄이면서)하는 것입니다. 즉, 업데이트될 새로운 정책을 다음처럼 표현할 수 있습니다.

식(6)의 의미는 식(5) 로부터 얻은 실제 새로운 정책의 성능은 그 새로운 정책을 $L$ (surrogate object) 이라는 함수에 대입한 값과 비교하였을 때, 적어도 $\frac{2\epsilon\gamma}{(1-\gamma)^{2}}\alpha^{2}$보다 성능이 감소하지 않음을 보장해줍니다.
이제 새로운 정책의 퍼포먼스의 lower bound를 구하였으므로, lower bound를 최대화시켜 퍼포먼스를 최대화할 수 있게 되었습니다.
3. Monotonic Improvement Guarantee for General Stochastic Polices
식(5) 에 등장하는 mixture policy는 일반적이지 않고 따라서 거의 쓰이지않는 비실용적인 방법입니다. 따라서 식(5)를 좀 더 일반적인 확률론적 정책에 관해 표현해야합니다. 본 논문에서는 $\alpha$를 old 정책 $\pi$와 new 정책 $\widetilde{\pi}$분포간의 거리의 지표 중 하나인 Total Variation Divergence를 사용하여 나타내어도 식 (6)이 성립함을 증명하였습니다. 조금 더 자세하게 $\alpha$를 풀어보면, 두 정책 분포의 각 상태마다 Total Variation Divergence 계산하였을 때, 가장 큰 Total Variation Divergence로 $\alpha$를사용합니다. 즉, $\alpha$로 다음을 사용합니다.
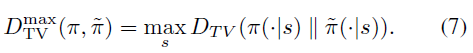
$\alpha$를 이렇게 대체하고, 식 (6)을 재정리하면 최종적으로 다음과 같은 정리가 완성됩니다.

Theorem 1.로 인해 우리는 이제 일반적인 확률론적 정책에 사용이 가능하며, 정책 갱신에 대한 lower-bound를 얻게 되었습니다. 본 논문에서는 식(8)을 두 가지 방법으로 증명하였는데, 첫 번째 방법은 KaKade & Langford의 결과를 조금 더 확장하여 증명하는 방법이고, 두 번째 방법은 섭동이론(Perturbation Theory)로 증명하는 방법입니다. 두 방법 모두 본 논문의 Appendix에서 잘 설명하고 있습니다.
다음으로 Total Variation Divergence는 KL Divergence보다 작기 때문에 lower-bound를 Total Variation Divergence 대신 KL Divergence로 표현할 수 있습니다. 즉, 아래의 식이 성립합니다.
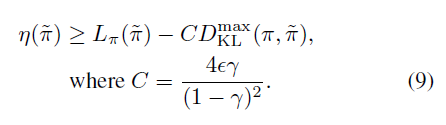
이제 이 lower-bound를 최대화 한다는 전략을 사용하여, 퍼포먼스의 향상을 보장하는 정책을 구하는 알고리즘을 봅시다.

알고리즘은 정책을 lower-bound를 최대화 시키는 정책으로 계속 수렴할 때 까지 반복적으로 갱신하게 됩니다.이러한 알고리즘은 minorization-maximization (MM) 알고리즘의 한 종류입니다. MM알고리즘에서 사용하는 용어로 $M_{i}$는 $\eta$를 minorize하는(그리고 $\eta$과 $\pi_{i}$에서는 같고) surrogate function을 의미합니다. 위 알고리즘을 시각적으로 표현하면 아래 그림과 같습니다.

4. Optimization of Parameterized Polices
이전 장에서 언급한 알고리즘은 이론적으로는 훌륭하지만 실제로 적용하기가 어렵습니다. 따라서 이번 장은 유한한 샘플 수와 임의의 파라미터화(finite sample counts and arbitrary parameterizations)에 대해서 작동하는 실용적인 알고리즘을 고안할 것입니다. 또한 이제부터 계속 벡터 $\theta$하에 parameterized policy $\pi_{\theta}(a|s)$에 대해서 생각해 볼 것이기에 표기법에 있어서 다음과 같은 축약 표기법을 사용하겠습니다.

이전 장에서 실제 objective인 $\eta$를 증가시키기 위해 다음의 lower-bound를 최대화 시키는 전략을 사용하였습니다.

실제로 위 최적화 문제를 그대로 풀어 새로운 정책을 찾는다면, 정책의 변화는 매우 작게 됩니다. 즉 정책 변화의 step-size가 매우 작아질 수 있습니다. step-size가 매우 작다면 수렴하는데 걸리는 시간과 샘플들이 많이 필요하기에 우리는 어느정도 step-size를 크게 하여 업데이트를 하고 싶습니다.

실용적으로 좀 더 큰 step-size를 가지게 할 수 있는 한 방법은 KL Divergence를 새로운 정책과 이전 정책의 제약식으로 표현하는 것 입니다. 이를 이용하여 식 (9)를 아래와 같은 최적화 문제로 변환할 수 있습니다.

식(11)을 보면 KL Divergence의 값인 이전 정책과 새로운 정책의 거리를 ‘trust region'이라고 불리우는 크기로 제약을 겁니다. trust region은 학습을 할 때 수렴의 방향성을 벗어나지 않는 크기라고 생각하실 수 있습니다. 즉, trust region이 너무 커서 새로운 정책과 기존 정책의 KL Divergence가 커지는 것을 용인한다면, 최적 정책으로의 수렴은 보장할 수 없게됩니다.
한편 본 논문에서는 여기서 또 한번 근사를 진행을 합니다. 왜냐하면 식 (11)에서는 모든 state에 대해 KL Divergence의 최댓값을 찾아야하기 때문입니다. 이 작업을 간단하게 하기 위해 KL divergence의 최댓값을 평균값으로 heuristic하게 근사합니다.

따라서 식 (11)은 최종적으로 다음과 같은 최적화 문제를 푸는것으로 바뀝니다.

결국 TRPO는 식(12)를 푸는 알고리즘이라고 볼 수 있습니다.
5. Sample-Based Estimation of the Objective and Constraint
지금까지 파라미터로 근사된(예를 들어 신경망 혹은 선형 근사) 정책의 퍼포먼스의 기댓값을 최대화하기 위해 식(12)와 같은 제약 최적화 문제를 구했습니다. 이제 (12)를 토대로 최적 정책을 찾기만 하면 됩니다. 그런데 문제가 있습니다. 우리가 오라클과 같은 신적인 존재가 아니기에 샘플들의 정확한 평균 및 분포를 알 수가 없습니다. 따라서 에이전트와 환경의 상호작용을 통해 얻은 샘플을 가지고 평균 및 분산을 추정할 수 밖에 없는 추정의 문제가 생깁니다. 이 추정을 어떻게 하느냐에 따라 추정량과 그 추정량의 분산에 편향이 있을 수도 없을 수도 있습니다.
이번 장에서는 ‘몬테 카를로' 를 통해 식(12)의 목적 함수(L, objective function)와 제약 함수(D, constraint function)를 어떻게 추정할지에 대한 내용을 담고있습니다.
가장 먼저 $L_{\theta_{old}}$를 살펴보겠습니다.. $L_{\theta_{old}}$를 풀어서 식(12)를 다시 나타내면,

과 같습니다. 우리는 어떻게든 샘플 기반으로 이 제약식을 최적화해야 하기 때문에(우리는 오라클이 아니기 때문...) 식(13)을 다음과 같이 수정해야합니다.
먼저 $\sum_{s}^{}\rho_{\theta_{old}}(s)[...]$를 평균 $\frac{1}{1-\gamma}\mathbb{E}_{s\sim p_{\theta_{old}}}[...]$으로 바꿉니다. 그리고 advantage 값 $A_{\theta_{old}}$을 Q 값인 $Q_{\theta_{old}}$로 바꿉니다. 마지막으로
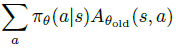
항을 importance sampling으로 추정할 것입니다. 이 때 behavior policy (sampling distribution)은 $q$로 표현할 것입니다. 이렇게 항들을 바꿔주면 식 (13)은 다음과 같이 변하게 됩니다.

이로써 최적화 문제를 평균에 관한 값으로 바꾸었고, 각 샘플들의 평균은 불편항 추정치이므로(비록 분산은 클지라도) 샘플들을 이용하여 최적화 문제를 풀 수 있게 되었습니다.
본 논문에서는 두 가지의 샘플링 방법을 소개하였습니다. 하나는 Single Path이고, 나머지 하나는 Vine이라는 방법입니다.
식 (14)는 TRPO알고리즘의 최종 모습이라고 할 수 있겠습니다.
5.1 Single Path
단순하지만 빠르고 효과적인 방법입니다. Single Path는 먼저 초기 상태 분포 $s_{0}\sim \rho_{0}$로부터 초기 상태 $s_{0}$를 설정하고 정책 $\pi_{\theta_{old}}$에 따라 시뮬레이션하여 trajectory $s_{0},a_{0},s_{1},a_{1},...,s_{T-1},a_{T-1},s_{T}$를 얻습니다. 정책 $\pi_{\theta_{old}}$에 따라 시뮬레이션을 하기에 behavior policy $q$는 $\pi_{\theta_{old}}$가 됩니다. 이 trajectory를 바탕으로 모든 state-action pair의 $Q_{\theta_{old}}(s,a)$를 구하게 됩니다.

5.2 Vine
앞서 소개한 Single Path는 하나의 샘플 trajectory에 대해서만 추정하므로 분산이 크다는 단점이 존재합니다. 두 번째 방법인 Vine은 이러한 단점을 보완하기 위해 고안되었습니다. Vine은 먼저 Single Path와 마찬가지로 먼저 초기 상태 분포 $s_{0}\sim \rho_{0}$로부터 초기 상태 $s_{0}$를 설정하고 정책 $\pi_{\theta_{i}}$에 따라 여러개의 trajectory를 생성합니다. 그리고 이 trajectory로부터 N개의 상태를 고릅니다. 즉 $s_{1},s_{2},...,s_{N}$를 고릅니다. 그리고 이 각각의 상태에 대해 behavior policy $q$에 따른 K개의 행동을 취합니다. 무슨 말인지 잘 모르시겠죠..? 그림을 통해 이해해봅시다.

그림을 보면 두 개의 trajectory를 만들고 이 trajectory의 state중 몇몇 state에 대해 rollout을 만듭니다.(예를 들어 state1, state15) 이때 각 state에 대해 action을 다르게 하여 rollout을 만듭니다. 따라서 다음과 같은 pair를 얻습니다.
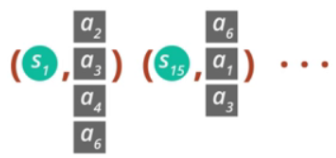
rollout은 각 state의 K개의 action에 대하여 진행된다고 하였으니, 이 K개에 대한 rollout을 분석하는 것이 1개의 rollout을 분석하는 것보다(Single Path 방법) 훨씬 분산이 적겠죠? 논문에서 이렇게 분산을 줄이기 위해 넝쿨(vine)처럼 샘플링을 하는 방법을 Vine이라고 명명했습니다.
만약 작고 유한한 엑션 공간이라면 주어진 상태에 대해 모든 가능한 행동들에 대해 rollout을 진행할 수 있습니다. 그렇다면 surrogate objective $L_{n}(\theta)$의 추정치는 다음과 같이 정규화될 수 있습니다.

하지만 Vine 방법은 계산량이 너무 많은 등 단점이 명확하기에 실용적인 방법은 아닙니다.
6. Practical Algorithm
지금까지 우리의 최적화 아이디어를 바탕으로 Single Path와 Vine이라는 두 가지 알고리즘을 제안하였습니다. 이 두 알고리즘은 다음과 같은 방향으로 진행됩니다.
- Single Path알고리즘이든 Vine알고리즘이든 샘플링을 통해 몬테카를로 추정치를 얻습니다.
- 모은 샘플들을 평균화하여 식(14)의 objective와 constraint를 구합니다.
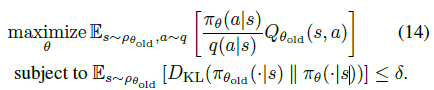
- policy 파라미터를 조금씩 반복적으로 갱신함으로써 이 제약 최적화 문제를 풉니다. 이 문제를 푸는 다양한 방법이 있지만, 본 논문에서는 line search와 conjugate gradient 방법을 통해 풀었습니다.
위 절차 중 3번을 다시 봅시다. 저자는 conjugate gradient방법을 사용했다고 했는데, 왜 이 방법을 택했을까요? 식 (14)을 잘 보면 KL제약식을 푸는 것이 Natural Gradient Descent와 유사함을 알 수 있습니다. (KL의 Hessian이 바로 Fisher Information Matrix 이니까요! 이해가 잘 안되시면 제가 포스트한 Natural Policy Gradient 논문 리뷰를 봐주시길 바랍니다.)
그래서 이 FIM(Fisher Information Matrix)를 구하기 위해
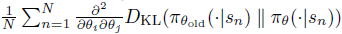
를 사용합니다. 이 추정치는 모든 action을 적분한 것이기에 각 상태에 따른 특정한 action에 의존적이지 않습니다.
본 저자도 이 유사성을 이용하여 Natural Gradient Descent 기반의 방법으로 문제를 풀려고 시도하였습니다. 그러나 이 방법은 연산량이 매우 높습니다.(Fisher Information Matrix의 저장 및 역행렬을 구해야 하기 때문입니다.) 따라서 본 논문의 저자들은 이를 conjugate gradient 방법으로 근사시켜 푸는 방법을 택하였던 것 입니다. 보다 자세한 내용은 Appendix C에서 다루겠습니다.
여하튼 결과적으로 objective는 1차근사하고 constraint는 2차근사(Hessian)하여 최적화 문제를 풀게됩니다. 이와 관련된 내용은 다음장에서 바로 확인하실 수 있습니다.
7. Connections with Prior Work
사실 Natural Policy Gradient (Kakade, 2002)는
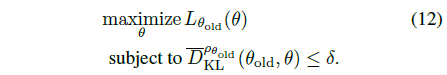
식(12)를 풀기위한 업데이트의 한 방법입니다. Natural Policy Gradient는 L을 선형근사하고 KL 제약식을 이차근사 하여 표현 합니다. 다음 처럼요.

그리고 업데이트 룰은 다음과 같습니다.

(왜 이러한 업데이트 룰을 얻는지는 지난 포스트(Natural Policy Gradient) 참고)
위 업데이트 식에서 $\frac{1}{\gamma}$는 step size 파라미터로 취급됩니다. 이는 본 논문의 방법과 조금 다릅니다. 왜냐하면 본 논문에서는 각 업데이트마다 제약을 걸어주기 때문입니다.(line search 등을 통해) 또한 본 논문의 방법을 사용하였을 때 더 좋은 성능을 보였습니다. (아마 근사에 의한 오차를 줄일 수 있어서 일 것입니다.)
그리고 만약 Natural Policy Gradient가 아닌 일반적인 Policy Gradient방법을 사용한다면, 다음과 같이 $l_{2}$ 제약을 통해 나타낼 수 있을 것입니다.

8. Experiments
8.1 Simulated Robotic Locomotion
먼저 MuJoCo simulator를 이용하여 robotic locomotion 실험을 하였습니다.
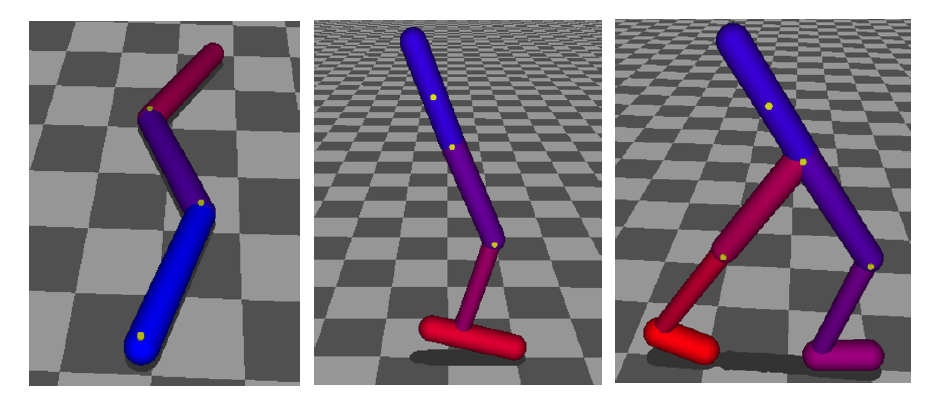
각 실험은 Cartpole, Swimmer, Hopper, Walker에 대해서 실험을 진행하였고 아래는 그 결과입니다.

TRPO 알고리즘(Single Path & Vine)이 다른 알고리즘에 비해 더 높은 성능을 보여줌을 확인할 수 있습니다.
8.2 Playing Games From Images
저자들은 Atari 게임에 대해서도 실험을 진행하였습니다. 결과는 아래와 같습니다.

Appendix A: Proof of Policy Improvement Bound
이 장에서는 본 논문에서 사용한 수식

이 왜 성립하는지에 대해 알아보겠습니다.
먼저 이 장의 증명 과정에 있어서 저의 생각을 추가로 담은 부분이 있다는 점이 있음을 염두해 주시고 봐주시면 감사하겠습니다.
step 1. 두 정책의 성능 차이를 수식으로 나타내기.
먼저 다음의 Lemma가 성립함을 보입니다.
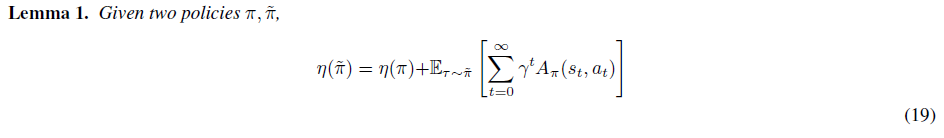
위 식(19)는 서로 다른 두 정책에 대해서 성능의 차이를 time-step 마다의 advantages의 합으로 나타낼 수 있음을 보여줍니다. 여기서 notation 타우($\tau$, tau)는 정책을 따르는 궤적 $\tau:=(s_{0},a_{0},s_{1},a_{1},...)$ 을 의미하고, $\mathbb{E}_{\tau\sim \widetilde{\pi}}[...]$의 아래 첨자는 행동들이 정책 $\widetilde{\pi}$에 따라 샘플링되어 궤적 $\tau$를 생성하는 것을 의미합니다.
식 (19)의 증명은 다음과 같습니다.

$A_{\pi}(s,a)=\mathbb{E}_{s^{'}\sim P(s^{'}|s,a)}[r(s)+\gamma V_{\pi}(s^{'})-V_{\pi}(s)]$이기 때문에,
이기 때문에,
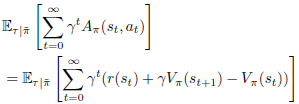
이 성립합니다. 그런데 $\sum_{t=0}^{\infty }\gamma^{t}(\gamma V_{\pi}(s_{t+1})-V_{\pi}(s_{t}))$은
은 $-V_{\pi}(s_{0})$와 같기 때문에 아래가 성립합니다.

계속 전개해보면,

가 되며, 이는 식(19)와 같습니다.
이제 이 결과를 조금 바꿔서 표현해보겠습니다. 먼저 $\overline{A}(s)$를 상태 $s$에서 정책 $\pi$를 따를 때의 $\widetilde{\pi}$의 advantage의 기댓값이라고 한다면, 즉,
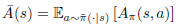
라고 한다면, 위의 Lemma 1은 다음처럼 쓸 수 있습니다.
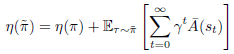
그리고 $L_{\pi}$에 대해서는 아래와 같습니다.

step 2. 두 정책이 얼마나 다른지 척도 정하기
$L_{\pi}(\widetilde{\pi})$는 샘플링하는 정책이 바뀌었으므로, $\eta(\widetilde{\pi})$와 $L_{\pi}(\widetilde{\pi})$의 성능 차이가 얼마나 다른지 알려면 앞서 두 정책 $\pi$, $\widetilde{\pi}$이 얼마나 다른지에 대한 척도가 필요할 것입니다. 본 논문에서는 서로 다른 정책에서 샘플링 되는 행동들의 결합분포의 확률을 이용하여 척도를 매깁니다. 구체적으로 알파-결합 정책 쌍(alpha-coupled policy pair)이라고 표현되는 두 정책의 결합분포는 다음처럼 정의됩니다.
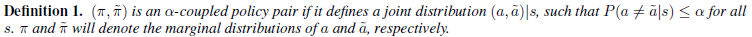
즉, 알파-결합 정책 쌍은 (어떠한 상태에서든) 두 행동(서로 다른 두 정책에서 샘플링된)이 다를 확률이 $\alpha$보다는 작음을 의미합니다. 반대로 말하면 서로 다른 두 정책하에서 같은 행동이 나올 확률은 최소한 $1-\alpha$은 됨을 의미합니다. 본 논문에서는 이렇게 $\alpha$를 통해 두 정책이 얼마나 다른지에 대한 척도를 정합니다.
step 3. 두 정책이 다른 정도의 척도를 통해 $\eta(\widetilde{\pi})$와 $L_{\pi}(\widetilde{\pi})$의 성능 차이의 하한 구하기
이제 본격적으로 두 성능의 차이를 구해봅시다. 먼저 다음의 Lemma를 증명하면서 시작합니다.



($\mathbb{E}_{a\sim \pi}[A_{\pi}(s,a)]=0$이기 때문에)
그리고 위 식을 다른 정책에서 샘플링된 두 행동이 같을 때와 같지 않을 때로 나누어 표현하면,

행동이 같다면 두번째항은 소거되므로,

가 됩니다. 이제 이 식의 upper bound를 구해보겠습니다.

따라서 최종적으로 Lemma 2.가 성립합니다. 즉,

이제 다음의 Lemma가 성립함을 증명해야합니다.

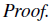
$n_{t}$가 timestep t 동안 두 행동이 서로 다른 횟수 즉, $a_{i}\neq \widetilde{a_{i}}$의 횟수라고 정의하면 $\mathbb{E}_{s_{t\sim \widetilde{\pi}}}[\overline{A}(s_{t})]$은 다음처럼 나타낼 수 있습니다.
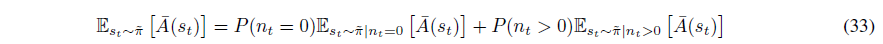
비슷하게 정책 $\pi$를 통해 샘플링된 기댓값으로 바꾸면 다음이 성립합니다.
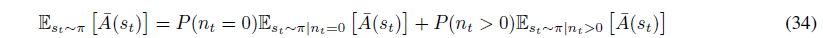
만약 $n_{t}=0$이라면 모든 행동들이 같을 때를 의미하므로 다음 항들이 같습니다.
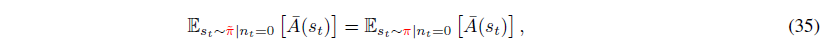
식(35)를 이용하여 식(33)에서 식(34)를 빼면 다음을 얻습니다.

한편 $\alpha$는 서로 다른 두 정책을 따랐을 때, 모든 상태에서 두 행동이 다를 확률의 상한값을 나타내므로, timestep $t$ 동안 $n_{t}=0$일 확률은

를 만족합니다. (한 상태에서 두 행동이 같을 확률은 최소한 $1-\alpha$이고 $t$시간동안 모든 행동이 같은 경우의 확률이기 때문에) 그래서 결국 다음을 얻습니다.

그리고 식 (28) 덕분에 다음이 성립합니다.
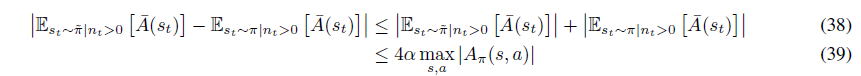
그런데 식(37)과 식(39)를 식(36)에 대입하면 다음을 얻게됩니다.
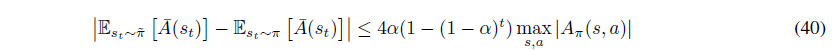
거의 다 왔습니다. 마지막으로
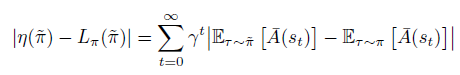
임을 이용하여 식을 쭉 전개해나가면,

여기서

입니다.
step 4. 척도($\alpha$)를 Total Variation Divergence(TV divergence)로 바꾸기
우리는 최종적으로 $\alpha$를 TV divergence로 바꾸고 싶습니다. 그러기 위해선 우리가 정의했던 coupled random variable과 TV divergence가 일치함을 보여야합니다.
먼저 $p_{X}$와 $p_{Y}$가 $D_{TV}(p_{X}\parallel p_{Y})= \alpha$의 분포라고 가정합시다. 그러면 주변 분포가 $p_{X}$, $p_{Y}$이고 $X=Y$일 확률이 $1-\alpha$인 결합 분포 $(X,Y)$가 존재합니다.
[Levin et al., 2009]을 보면

인 두 정책이 있다면, 우리는 이 두 정책 $(\pi, \widetilde{\pi})$ 의 $\alpha$-coupled pair를 정의할 수 있다고 합니다. 그래서 본 논문에서는 $\alpha$값으로

을 사용합니다. 결국 최종적으로 다음 정리가 성립됩니다.

Appendix C: Efficiently Solving the Trust-Region Constrained Optimization Problem
이 장에서는 Natural Gradient Descent에 관한 내용이 주를 이루니 만약 Natural Gradient Descent를 잘 모르신다면 지난 포스트를 보시는 것을 추천드립니다.
Appendix C에서는 우리의 최종 목적인 식 (14)를 어떻게 효율적으로 풀 것이냐에 대한 내용을 담고 있습니다.
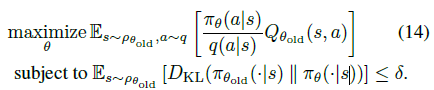
다시 말해 아래식,

을 효율적으로 푸는 방법을 알아봅시다.
이 장에서 소개할 방법은 크게 두 가지 step을 가집니다.
(1) objective를 선형근사하고, KL constraint 항을 이차근사하여 search direction(어느 방향으로 갱신할 지)을 계산합니다. (이렇게 근사하여 최적화를 풀면 해는Natural gradient Descent 방법으로 구한 해와 같습니다)
(2) 이 방향에 대해 line search를 함으로써 비선형인 제약조건을 만족함과 동시에 비선형인 objective의 성능을 보장해주며 업데이트를 합니다.
먼저 search direction은 방정식
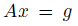
를 품으로써 얻을 수 있습니다. (A는 Fisher Information Matrix, FIM)입니다. 그리고 KL 제약식의 이차근사는 다음과 같습니다.

여기서 A는 마찬가지로 FIM이며

와 같습니다. 만약 매우 큰 스케일의 문제라면 FIM을 저장하고 계산하는데 시간이 매우 많이 걸릴 것입니다. 하지만 conjugate gradient algorithm을 사용한다면

식을 효율적으로 계산할 수 있습니다. (시간복잡도가 세제곱인 A의 역행렬을 구할 필요가 없으므로)
이러한 방법으로 어찌저찌 search direction을 구했으면(C.1에서 방법 소개), 그 다음 할 일은 얼마나 많이 step-size를 줄지 정하는 것입니다. maximal step length를 $\beta$라고 합시다. 그러면 $\theta + \beta s$는 KL 제약 조건을 딱 만족해야 할 것입니다. 즉 다음을 만족합니다.
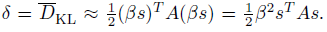
이 식을 토대로 $\beta$를 구해보면,
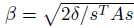
입니다. 특히 $s^{T}As$항은 Single Hessian 벡터곱으로 계산되어질 수 있고, 이는 conjugate gradient algorithm으로 바로 구할 수 있습니다.
이제 maximal step size $\beta$를 구했으니, step size의 크기가 $\beta$를 넘기지는 않되, 갱신에 적합한 size를 정해야합니다.(근사에 의한 error때문에 가끔 $\beta$가 매우 커질 수 있기 때문입니다.) 본 논문에서는 이를 단순히 line search를 통해 구현하였습니다.
C.1 Computing the Fisher-Vector Product
다시 돌아와서 search direction을 구해봅시다. 그런데 search direction을 구하기 위해서는 FIM의 역행렬을 구해야하는데 시간이 너무 많이 걸린다고 하였습니다. 그래서 저자는 두 개의 트릭을 제안합니다.
첫 번째 트릭은 Fisher-Vector Product $Hv$를 구하는데 사용됩니다. 일반적으로 이차 미분의 헤시안 꼴인 H(FIM)을 직접구하기는 까다롭습니다. 그래서 이 헤시안 하나를 구하는 것이 아닌, 헤시안과 벡터의 곱(matrix-vector product)을 통째로 구하는 방법을 사용합니다. Natural Gradient Descent는 KL의 헤시안임을 이용하면 다음을 얻을 수 있습니다.

여기서 $(\nabla_{\theta}\overline{D}_{KL}(\theta\parallel \theta_{k}))^{T}$과 $\nabla_{\theta}((\nabla_{\theta}\overline{D}_{KL}(\theta\parallel \theta_{k}))^{T}x)$는 딥러닝 라이브러리의 Autograd를 이용하면 쉽게 구할 수 있습니다. 이 트릭은 maximal step length
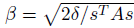
를 편리하게 계산할 수 있게 만들고, 또한 다음에 소개할 conjugate gradient method에도 사용됩니다.
두 번째 트릭은 앞에서 conjugate gradient method를 사용하여 search direction을 구하는 것입니다.
conjugate gradient method는 일반적으로 Ax=b 를 만족하는 x를 구하는데 사용되는 방법입니다. 이때 A의 역행렬을 직접적으로 구하는 것이 아닙니다. 이 방법은 A에 대한 내적 공간을 정의한 뒤에 이 공간에서 직교하는 기저들을 이용하여 x를 구하는 방법입니다. 이 방법은 x의 차원이 n 차원일 때, n번의 iteration 이내에 수렴함이 보장됩니다. 본 논문에서는 iteration이 10일 때 좋은 결과를 얻었다고 말합니다. 켤레 기울기법(conjugate gradient method)에 대해서는 설명하지 않겠습니다만 조금만 구글링을 하시면 아실 수 있는 내용입니다.
켤레 기울기법은 일반적으로 Ax=b 를 만족하는 x를 구하는데 사용된다고 언급하였는데, 여기서 A는 H(FIM), b= g가 되겠죠. 여기서 첫 번째 트릭을 사용하여 Ax(=Hx)을 구할 때 H를 따로 구하는 것이 아닌 matrix-vector product를 이용하여 통째로 구하게 됩니다.
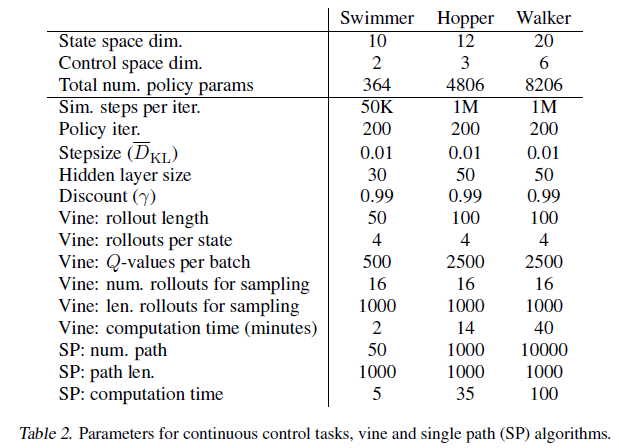
Appendix E: Experiment Parameters
마지막 장은 본 실험에 사용된 하이퍼 파라미터 정보를 보여줍니다.

리뷰를 마치며...
지금까지 TRPO의 이론적 배경을 살펴보았습니다. 매우 수학적인 내용을 담고 있기에 이해하는 데 많은 시간이 필요했습니다. 또한 TRPO를 직접 구현할 때 다양한 트릭들을 사용해야해서(matrix-vector product, conjugate gradient method, natural gradient descent, line-search 등등…) 매우 힘들었습니다. 하지만 논문을 다 읽고 알고리즘을 구현해보고 잘 돌아가는 것을 보니 꽤나 보람찼네요. 다음 리뷰는 본 논문의 저자인 John Schulman의 후속작인 PPO를 해볼까 합니다. PPO는 TRPO의 이론적 배경을 계승하되 좀 더 심플하게 그러나 더 성능이 좋도록 변형시킨 알고리즘입니다.
'Paper Review' 카테고리의 다른 글
| Planning with Goal-Conditioned Policies (2019) 논문 리뷰 (4) | 2023.05.14 |
|---|---|
| Reference Learning and Control as Probabilistic Inference: Tutorial and Review 논문 리뷰 (4) | 2022.06.12 |
| Variational Adversarial Imitation Learning (VAIL) 논문리뷰 (2) | 2022.02.26 |
| Natural Policy Gradient 논문 리뷰 (1) | 2022.02.14 |
| Generative Adversarial Imitation Learning (GAIL) 논문리뷰 (8) | 2021.12.29 |



