리뷰 작성: 김장원 / 석사과정 (jangwonkim@postech.ac.kr)
0. 시작하기 전에 알면 좋은 것들.
1 장에서는 본 논문을 읽기 전에 알아야 할 것들을 정리하였습니다. 사실 이번 장만 완벽히 이해하시면 본 논문의 대부분을 이해하셨다고 해도 과언이 아닙니다. 이 장의 내용은 Agustunus Kristiadi's Blog를 참고하여 작성하였습니다. 참고한 블로그의 링크는 https://agustinus.kristia.de/techblog/2018/03/11/fisher-information/ 입니다.
0-1. Fisher Information Matrix
첫 번째로 알아야 할 내용은 ‘피셔 정보 행렬' 입니다. 먼저 피셔 정보란 관측 가능한 확률 변수X의 정보의 양을 측정하는 한 척도입니다. 여기서 확률 변수의 정보를 구체적으로 말하기 전에, 우선 이 정보는 확률 변수X의 분포와 관련이 있다고 정도만 말하겠습니다. 그리고 이 확률 변수 X는 θ로 매개화된 모델로부터 얻게 됩니다. 즉, 피셔 정보란 θ로 매개화된 모델로부터 얻어지는 확률 변수 X의 정보이고, 이 정보는 이 모델의 분포인 $p(x|\theta)$와 관련이 있습니다.
자, 이제 다음과 같은 문제를 생각해 봅시다. 우리는 지금 θ로 매개화된 모델이 있습니다. 즉, 이 모델은 $p(x|\theta)$의 분포를 가지고 있다고 말할 수 있습니다. 빈도주의자 관점에서 $x$의 확률을 높이기 위해 $p(x|\theta)$를 최대화시키는 $\theta$를 찾는 것을 목표로 합니다. 다시 말해 likelihood $p(x|\theta)$를 최대화하고 싶습니다. 이에 우리는 $\theta$를 찾기 위해 학습을 진행하려고 합니다. 또한 $\theta$에 대한 추정이 잘 진행되고 있는지 평가하기 위해 다음과 같은 score 함수를 설정할 수 있습니다.
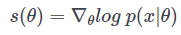
이 score 함수 $s(\theta)$는 log-likelihood의 경사도와 같습니다. 이 score 함수는 우리 모델에 대해 기댓값이 0이라는 성질을 가지고 있습니다. 즉,

입니다. 기댓값이 0이 되는 성질은 후에 유용하게 사용될 것이기에 기억해 주시길 바랍니다. 증명은 아래와 같습니다.

하지만 본론으로 다시 돌아와서, 이 score 함수를 통해 우리의 추정을 얼마나 확신할 수 있을까요? 이 질문에 답하기 위해서는 추정 값에 대한 "불확실성"에 대한 척도를 정의해야 합니다. 그리고 이 척도로 아래 식 처럼 우리 모델에 대한 score의 공분산을 사용할 것입니다.
$\mathbb{E}_{p(x|\theta)}[(s(\theta)-0)(s(\theta)-0)^{T}]$
맨 처음 언급했던 피셔 정보(Fisher Information)는 위 식과 같습니다. 다시 말해, 피셔 정보(Fisher Information)는 score 함수의 공분산과 같습니다. $\theta$는 벡터이므로 피셔 정보는 행렬 형태를 가지게 됩니다. 한편 score함수는 모델 분포의 log-likelihood의 경사도 였으므로, 피셔 정보 행렬(Fisher Information Matrix)을 아래와 같이 표현할 수 있습니다.
$\mathbb{E}_{p(x|\theta)}[\nabla log\ p(x|\theta)\ \nabla log\ p(x|\theta)^{T}]$
그러나 log-likelihood의 기댓값을 계산하는 것은 매우 복잡하므로, 우리는 피셔 정보 행렬 $F$를 우리의 데이터 샘플을 통해 근사하는 것이 편리합니다. 아래 식 처럼 말이죠.
$\frac{1}{N}\sum_{i=1}^{N}\nabla log\ p(x|\theta)\ \nabla log\ p(x|\theta)^{T}$
Fisher와 Hessian의 관계
우리가 알 수 있는 한가지 놀라운 성질은, 앞에서 얻은 피셔 정보 행렬$F$는 우리 모델의 log-likelihood에 대한 음의 Hessian 기댓값(negative expected Hessian)과 같다는 것입니다. 이 성질에 대한 증명은 아래와 같습니다.
$Proof$
모델의 log-likelihood의 Hessian은 log-likelihood의 경사도(gradient)의 쟈코비안과 같으므로,

양 변에 기댓값을 취해주면,

따라서 다음을 얻습니다.

이 결과는 기하학적으로 피셔 정보 행렬 $F$는 모델 분포의 log-likelihood의 곡률(curvature)를 측정하고 있는 것을 말해줍니다. (Hessian은 함수의 이차미분을 나타내기 때문입니다.)
지금까지 우리는 피셔 정보 행렬을 scroe 함수의 공분산으로 정의하였고, 이렇게 정의함으로써 피셔 정보 행렬은 음의 log-likelihood의 Hessian의 기댓값과 같으므로 곡률 행렬로 해석이 가능함을 보았습니다. 따라서 피셔 정보 행렬을 이차 미분을 통한 최적화 문제에 적용할 수 있습니다.
하지만 피셔 정보 행렬의 가장 놀라운 점은 KL-divergence와 연결점이 있다는 것입니다. KL-divergence는 두 분포간의 거리의 척도로 사용할 수 있죠. 그런데 피셔 정보 행렬과 Kl-divergence가 연결점이 있으니, 피셔 정보 행렬을 잘 사용하면 직접적으로 두 분포간의 거리를 줄일 수 있지 않을까요? 만약 그렇다면 일반적으로 $\theta$로 매개화된 모델은 파리미터의 경사도를 이용하여 $\theta$를 찾는데(일반적인 gradient descent 방법), 피셔 정보 행렬을 이용하면 파라미터공간이 아닌 분포 공간을 직접적으로 더듬어가며 최적의 $\theta$를 찾을 수 있지 않을까요?
Natrual Gradient Descent는 이러한 생각으로부터 탄생한 알고리즘입니다. 이제부터 피셔 정보 행렬과 KL-divergence간의 연결점을 중점으로 서술해보려 합니다.
0-2 Natural Gradient Descent
Distribution Space
Likelihood $p(x|\theta)$로 표현되는 모델을 최적하기 위해서는 보통 이 likelihood를 최대화하는 $\theta$를 찾아야 합니다. 이를 위해 손실 함수(loss function, $\mathcal{L}(\theta)$) 이라는 개념을 도입하고 이 손실 함수를 줄이는 쪽으로 학습을 진행하게 됩니다. 적당한 손실 함수들이 여럿 존재하지만, 빈도주의자 관점에서 이 손실 함수는 negative log-likelihood와 같습니다.
일반적인 gradient descent는 방향이$-\nabla_{\theta} \mathcal{L}(\theta)$인 크기가 작은 step을 반복적으로 취하여 최적화 하는 방법입니다. 이 방향은 파라미터 공간에서 현재 $\theta$에 대해 국소적으로 가장 가파른 방향입니다. 다시 말하지만 파라미터 공간에서 가장 가파른 방향입니다. 이를 수식으로 표현하면 다음과 같습니다.

위 식을 설명하자면, 국소적으로 파라미터 공간에서 가장 가파른 경사도 방형은 벡터 d를 선택하는 것임을 의미합니다. 이 벡터 d는 국소공간에서 loss function을 가장 작게 만드는 벡터입니다. 근데 이 국소공간($\epsilon$-neighborhood)의 크기는 유클리드 노름(Euclidean Nrom)으로 정의되었습니다. 즉, 일반적인 gradient descent는 파라미터 공간의 유클리디안 기하학을 이용하는 방법입니다.
한편, 우리의 목적은 loss function을 최소화하는 것(likelihood를 최대화하는 것)이고, 이 likelihood가 있는 공간에서 step을 취하는 것이 자연스럽습니다. 물론 이 likelihood는 파라미터 $\theta$를 통해 얻게 되지만요. 다시 말해, 파라미터 공간에서 step을 취하는 것보다는 likelihood만 있는 공간에서 step을 취하는 것이 더 자연스럽게 step을 취하는 방법입니다. 이 likelihood는 확률 분포이므로, 이 likelihood 공간은 분포 공간(distribution space)라고 불립니다.
이제부터 우리는 더 자연스러운 방법인, 파라미터 공간이 아닌 분포 공간에서 가장 가파른 경사를 택하여 step을 취하는 방법을 사용하고 싶습니다. 이러한 방법을 Natural Gradient Descent라고 불립니다.
분포 공간의 한 지점에서 가파른 경사를 찾기 위해서는 먼저 분포간의 거리를 나타내는 척도가 필요합니다. 다행히 우리는 KL-divergence라는 훌륭한 척도를 가지고 있습니다. KL-divergence는 두 분포가 얼마나 가까운지를 나타내는 척도로 사용되므로, 이제부터 KL-divergence를 두 분포간의 거리를 나타내는 척도로 사용하겠습니다. (물론 KL-divergence는 엄밀히 말하면, 대칭적이지 않기에 거리가 아닙니다. 하지만 국소영역에서는 대칭하게 수렴하기에 사용이 가능합니다.)
아래 그림에서 파라미터 공간에서 유클리디안 척도를 사용했을 때의 문제를 확인할 수 있습니다. 분산이 고정되어 있고 오직 평균만 파라미터화된 가우시안 분포를 생각해 봅시다.
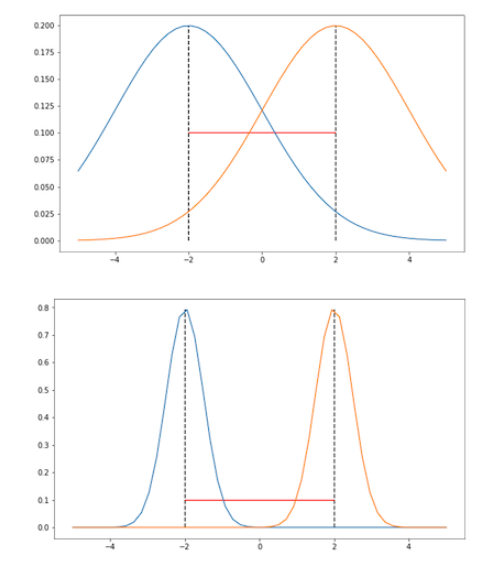
두 분포의 평균은 두 그림에서 모두 같지만, 분산은 서로 다릅니다. 분명하게 위 그림보다 아래 그림에서 분포의 차이가 더 크다는 것을 알 수 있습니다. 하지만 분포의 거리를 유클리디안 거리로 사용한다면, 위 그림과 아래 그림에서 두 분포의 거리는 같습니다. 우리의 직관과 매우 다른 결과를 보여주죠. 따라서 우리가 오직 파라미터 공간에서만 두 분포를 바라본다면, 이 파라미터들로 만들어지는 분포간의 정보를 상당 부분 잃게 됩니다. 이러한 이유로 파라미터 공간이 아닌 분포 공간에서 step을 취하는 Natural Gradient Descent 방법이 ‘자연스럽다'라고 말할 수 있는 것입니다.
Fisher Information and KL-divergence
이제 최종적으로 피셔 정보 행렬과 KL-divergence가 정확히 어떻게 연결되는지에 대한 대답을 하려고 합니다. 결론부터 말하자면, 피셔 정보 행렬은 분포 공간에서 거리를 KL-divergence 척도로 사용했을 때의 의 국소 곡률(local curvature)과 같습니다. 이는 피서 정보 행렬은 분포 공간에서 ‘‘리만 척도(Riemannian metric)를 사용하는 것이다 ‘‘라는 말과 같습니다.
좀 더 수학적으로 표현하면 피셔 정보 행렬$F$는 $\theta^{'}=\theta$에서 $\theta^{'}$에 대한 두 분포 $p(x|\theta),\ p(x|\theta^{'})$의 KL-divergence의 Hessian입니다. 증명은 아래와 같습니다.
$Proof$
KL-divergence는 엔트로피와 크로스 엔트로피 항으로 나뉘어 질 수 있으므로,

$\theta^{'}$에 대해 first derivative를 구하면,

이어서 second derivative를 구하면,

따라서, $\theta^{'}=\theta$에서 $\theta^{'}$에 대한 Hessian은

피셔 정보 행렬$F$입니다.
증명의 결과로 negative expected Hessian of log-likelihood는 피셔 정보 행렬$F$와 같음을 알 수 있습니다!
Steepest Descent in Distribution Space
이제 피셔 정보 행렬을 사용하여 gradient descent를 할 준비가 다 되었습니다. 가장 먼저 KL-divergence를 $\theta$근처에서의 테일러 급수로 표현할 것입니다. $d\to 0$일 때, 이 테일러 급수의 2차 항은 아래와 같습니다.

증명은 아래와 같습니다.
$Proof$
표기를 간략하게 하기 위해 $P(x|\theta)$를 $p_{\theta}$로 표기하겠습니다. 그러면 정의에 따라 KL-divergence의 2차항 까지의 전개는 아래와 같습니다.

여기서 첫 번째 항은 같은 분포이므로 KL-divergence 값이 0으로 수렴하게 됩니다. 또한 두 번째 항을 보면, 우리는log-likilihood의 경사도의 기댓값은 0임을 이 장에서 가장 처음 증명하였으므로 두 번째 항도 결국 0이 됩니다. 따라서 오른쪽 수식은 세 번째 항만 남게 됩니다. 따라서,
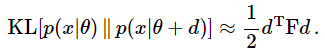
가 성립하게 됩니다.
이제 분포 공간 상에서 loss function $\mathcal{L}(\theta)$를 최소화시키는 $\theta$의 방향 $d$을 구해봅시다. 그런데 분포 공간에서는 KL-divergence의 변화가 가장 큰 방향이 바로 $d$라는 것을 알고 있습니다. 일반적인 gradient descent에서 파라미터 공간에서 유클리디안 거리를 이용하여 $d$를 구했다면 natural gradient descent는 분포 공간에서 KL 거리를 이용하여 이 $d$를 구한 것입니다. 이 새로운 방향 $d$를수식으로 표현하면 아래와 같습니다.

c는 어떤 상수입니다. 이 c를 이용하여 KL-divergence의 크기를 고정시킨 목적은 분포 공간을 곡률과 상관없이 일정한 속도로 움직이게 하고 싶기 때문입니다. 또 모델의 reparametrization에 대해 더욱 강인한(robust) 알고리즘을 만드는데 편리하기 때문입니다. 구체적으로 설명하면 natural gradient는 모델이 어떻게 파라미터화가 되었는지 상관없이 같은 분포의 변화를 만들게 됩니다. (알고리즘은 모델은 어떻게 parameterized되는지 보다는 이 parameter로부터 만들어지는 분포 공간을 더욱 신경 쓰게 됩니다.)
위 제약식은 아래와 같이 라그랑지안으로 표현이 가능합니다.

(KL-divergence는 테일러 급수의 두 번째 항으로 근사하였고, $\mathcal{L}(\theta+d)$는 테일러 급수의 첫 번째 항으로 근사하였습니다.) 이 최소화 문제를 풀기 위해 라그랑지안을 $d$에 대해 미분하고 이를 0으로 만드는 $d$를 구해봅시다.
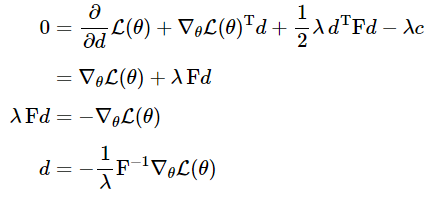
여기서 상수 $\frac{1}{\lambda}$는 learning-rate에 흡수 될 수 있기에 최종적으로 다음과 같은 경사도를 얻습니다.

네. 이것이 바로 Natrual Gradient 입니다!
Natural Gradient Descent 알고리즘의 전체적인 흐름은 아래와 같습니다.

하지만…
Natural gradient descent는 이론적으로 매우 훌륭한 알고리즘입니다. 하지만 딥러닝 모델같이 파라미터가 굉장히 많아진다면 피셔 정보 행렬 $F$를 얻고, 저장하고 역행렬을 구하는 등 연산이 매우 비싸집니다. 딥러닝에서 second-order 최적화가 인기가 없는 것도 비슷한 이유입니다.
이 문제를 해결하기 위해서 Fisher/Hessian을 근사해서 사용하는 것이 하나의 방안입니다. 예를 들어, Adam[1]같은 방법은 그라디언트의 첫 번째 모멘텀과 두 번째 모멘텀의 평균을 계산합니다. 여기서 두 번째 모멘텀이 피셔 정보 행렬을 근사한 것입니다. 근사된 피셔 정보 행렬은 대각 행렬이 됩니다. (대각행렬을 다루는 건 정말 쉽겠죠?) Adam은 매우 실용적이고 실제로 잘 작동하기에 신경망 최적화 문제에서 스탠다드로 사용되고 있습니다.
[1] Kingma, Diederik P., and Jimmy Ba. "Adam: A method for stochastic optimization."
여기까지가 "시작하기 전에 알면 좋은 것들"에 대한 내용입니다. 이제 본 논문을 본격적으로 파헤쳐 봅시다!
참고: 다음 paper[2]는 Natural Gradient Method를 더 깊이 이해하기 위한 훌륭한 지침서로 참고하실 수 있겠습니다.
[2] Martens, James. "New insights and perspectives on the natural gradient method." arXiv preprint arXiv:1412.1193 (2014).
A Natural Policy Gradient
저자: Sham KaKAde
Advances in Neural Information Processing Systems, 2002
1. Abstract
본 논문에서는 크게 다음과 같은 세 가지에 주목하며 전개됩니다.
1. 매개화된 공간에서 가장 가파른 경사도를 표현하는 natural gradient method를 소개합니다. 이전 장을 다 보셨다면 일반적인 gradient method가 아닌 natural gradient method가 왜 가장 가파른 경사도를 표현할 수 있는지 이해하실 수 있을 것입니다.
2. 더 나아가 본문에서는 gradient method가 파라미터의 값을 많이 변화시키지 못하더라도 natural gradient는 단순히 좋은 액션이 아닌 최적화된 그리디 액션을 취하는 방향으로 학습이 됨을 보여줍니다. 근사된 가치 함수를 사용할 때, 이러한 그리디 액션은 정책 반복에서 정책 향상 단계에서 선택되어 집니다.
3. 실험적으로 간단한 MDP환경과 Tetris 처럼 복잡한 MDP환경에서 성능이 크게 개선되었음을 보여줍니다.
2. Introduction
MDP문제를 해결하기 위해 policy-gradient method가 큰 관심을 받고 있습니다. 이 방법에서는 미래 보상의 그라디언트를 따라 정책을 개선시키게 됩니다. 그러나 불행히도 일반적인 gradient descent 방법은 non-covariant합니다.
non-covariant 벡터는 한 공간에서 기저들이 변화할 때, 같이 변화하는 벡터를 의미합니다. 예를 들어 속도 벡터를 생각해 봅시다. 속도의 단위를 km/s로 표현하는 공간이 있었는데, 이제 m/s로 표현하도록 공간이 변화한다고 생각해봅시다. 이 공간의 변화는 곧 기저의 변화를 의미하고 각 기저에 1000배 만큼 스케일업한 것과 같습니다. 이때 속도 벡터 역시 1000배 스케일 업 됩니다. 즉 공간 기저의 변화가 벡터의 변화에 영향을 끼칠 때, 그 벡터를 non-covariant 벡터라고 합니다.
그러니 "일반적인 gradient descent 방법은 non-covariant합니다. " 라는 말은, 파라미터 공간에서 gradient descent 방법은 파라미터에 의존적이라는 말과 같습니다. 파라미터에 의존적인 gradient descent 방법은 결국 policy 분포에 대한 가장 가파른 경사도가 되지 않을 수도 있습니다. (비록 policy가 파라미터에 의해 표현(realize)된다 할지라도요.)
그런데 우리는 이미 파라미터에 의존적이지 않은 gradient descent 방법을 배웠습니다. 바로 피셔 정보 행렬을 이용한 Natural gradient descent 방법이죠. 이 방법은 KL-divergence를 척도로 두 분포 간의 거리를 직접 계산하기 때문에 어떠한 파라미터로 표현되는 모델이든 같은 크기만큼의 경사도가 정해집니다. 이렇게 파라미터의 의존적이지 않은 경사도야말로 진정한 steepest descent 방향이라고 할 수 있을 것입니다.
3. A Natural Gradient
이번 장에서는 경사도를 일반적인 gradient가 아닌 natural gradient로 나타내겠다는 내용을 담고 있습니다.
이번 장은 이 포스팅의 맨 처음 "0. 시작하기 전에 알면 좋은 것들" 장을 읽으셨다면 자연스럽게 이해되는 장이라 생각되어 리뷰를 생략하겠습니다. 다만 다음의 질문에 답을 하실 수 없다면, 다시 꼼꼼히 포스팅을 보시는 것을 추천합니다.
- 파라미터 공간과 정책 분포 공간의 차이?
- 정책 분포 공간에서 거리의 척도로 KL-divergence를 사용하면, 왜 natural gradient는 $\widetilde{\nabla}\eta(\theta)\equiv F(\theta)^{-1}\nabla \eta(\theta)$가 되는지?
- 왜 정책 분포 공간에서의 steepest gradient (natrual gradient)는 파라미터에 의존적이지 않은지? 다시 말하면 왜 natural gradient는 covariant 벡터인지? (하지만 본 논문의 실험에서 natural gradient는 covariant하지 않습니다. 그 이유는 6장에서 밝힙니다.)
- Kakade는 왜 정책 분포 공간을 파라미터 공간상의 manifold 라고 표현하는지?
4. The Natural Gradient and Policy Iteration
이번 장에서 Kakade는 natural gradient하의 정책 개선과 정책 반복법(policy iteration)의 연결점을 보여줍니다.
이 때 사용되는 행동-가치 함수 $Q^{\pi}(s,a)$는 $\omega$를 파라미터로 사용하는 근사 함수 $f^{\pi}(s,a;\omega)$로 표현하겠습니다. (이 때 $f^{\pi}(s,a;\omega)$는 $Q^{\pi}(s,a)$를 충분히 잘 근사할 수 있는 함수라고 가정합니다.)
그리고 함수 $f^{\pi}(s,a;\omega)$는 다음과 같습니다.

함수 $f^{\pi}(s,a;\omega)$를 왜 하필 이렇게 정의했는지 그 의미를 잘 모르시겠다면, Compatible Function Approximation과 관련된 Sutton 교수님의 논문 "Policy Gradient Methods for Reinforcement Learning with Function Approximation"을 보시는 것을 추천드립니다.
4-1. Compatible Function Approximation
여하튼 $f^{\pi}(s,a;\omega)$를 통해 $Q^{\pi}(s,a)$를 잘 근사하기 위해서 다음과 같은 에러 함수를 설계합니다.

$Theorem 1.$ 이 때 에러 $\epsilon(\omega,\pi)$를 최소화 시키는 $\widetilde{\omega}$는 다음과 같다.

증명을 해보겠습니다.
$Proof$
$\widetilde{\omega}$는 에러를 가장 작게 만드는 파라미터이기에 $\partial \epsilon/\partial \omega_{i}=0$를 만족하는 값을 찾으면 됩니다. 따라서 아래 식을 세울 수 있습니다.
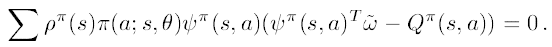
식을 더 전개하면 다음과 같습니다,
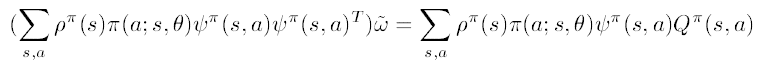
여기서, $\nabla \pi(a;s,\theta)=\pi(a;s,\theta)\psi^{\pi}(s,a)$이기 때문에, 위 식에서 우변은 다음과 같습니다.

이제 좌변을 보면,

이기 때문에, 좌변은 다음과 같습니다.

이제 앞서 구한 좌변과 우변을 같이 쓰면 아래와 같은 식을 세울 수 있고,

따라서 $\widetilde{\omega}$는 다음과 같습니다.

Q.E.D.
이 결과를 보면 최적의 $\widetilde{\omega}$는 natural gradient로 구할 수 있음을 확인할 수 있습니다. 이 장에서 Kakade가 말하고자 하는 부분은 만약 우리가 linear function으로 가치 함수를 근사한다면, 최적의 파라미터를 찾기 위해 natural gradient를 사용하게 된다는 것입니다.
아울러 이제부터 $F(\theta)^{-1}\nabla \eta(\theta)$를 간단히 $\widetilde{\nabla}\eta(\theta)$로 줄여 표기하겠습니다.
4-2. Greedy Policy Improvement
Kakade는 더 나아가 natural gradient와 탐욕적 정책 향상의 연결점에 관해 서술하였습니다. 근사 함수를 사용하여 탐욕적 선택을 한다는 말은 다음과 같은 행동 $a$ 를 선택한다는 말과 같습니다.
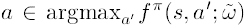
natural gradient는 사실 이런 최적의 행동을 찾는 방향으로 학습이 됩니다. 다시 말해 natural gradient단순히 좋은 행동을 선택하도록 움직이는 것이 아니라 탐욕적 행동을 선택하도록 움직입니다. 이를 증명하기 위해 먼저 정책 함수가 지수족(expoential family)인 특별한 경우를 생각해봅시다.
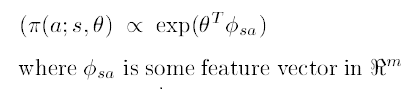
정책을 하필 지수족으로 근사한 이유는 이들이 affine geometry를 만족하기 때문입니다. affine geometry는 쉽게 말하면 선형 변환이라고 볼 수 있습니다. 선형변환은 각 기저들의 독립성을 보존 해줍니다. 기저들의 독립성을 보존시킨다는 말은 아래 그림을 보면 쉽게 이해하실 수 있습니다.
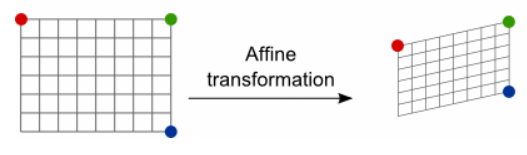
그림을 보면 변환을 하기 전이나 한 후나 각 기저들은 평행합니다. 다시 말해 기저들은 변함없이 독립성을 유지합니다. affine 변환은 이러한 특징이 있기 때문에, Kakade는 접선 벡터에 의한 점의 표현 역시 manifold 상에서 유지 될 것이라 생각하여(manifold 역시 같은 평면이기에) 정책을 지수족으로 표현한 것 같습니다.
하지만, 일반적으로 파라미터에 대한 정책 분포 공간은 휘어질 수 있기 때문에(파라미터 공간->정책 분포 공간 으로의 변환은 비선형 변환이기 때문입니다.) 파라미터 공간상에서의 접선 벡터는 정책 분포 공간(manifold된 공간)에서 일치하지 않을 수 있습니다.
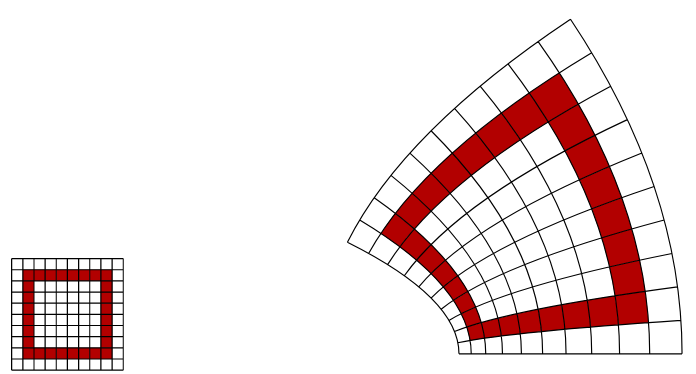
따라서 나중에 좀 더 일반적인(지수족으로 표현하지 않는) 케이스에 대해서 설명을 할 것입니다.
자, 이제 먼저 정책이 지수족일 때, natural gradient에서 step이 충분히 크다면 gradient의 갱신 방향은 탐욕적 행동을 선택하는 방향임을 보이겠습니다.
$Theorem 2.$ 정책이 지수족으로 표현되고 ( $\pi(a;s,\theta) \propto exp(\theta^{T}\phi_{sa})$ ), 또 $\widetilde{\nabla}\eta(\theta)$가 0이 아니고, $\widetilde{\omega}$가 근사 에러를 가장 작게 만든다고 가정해보자.
이 때 $\pi_{\infty}(a,s) = lim_{\alpha\to \infty}\pi(a;s,\theta+\alpha\widetilde{\nabla }\eta(\theta))$라면,
$\pi_{\infty}(a,s) \neq 0 \ \ \ iff\ \ \ a\in argmax_{a^{'}}f^{\pi}(s,a^{'};\widetilde{\omega}) 이다.$
$Proof$
저번 결과에서 알아보았듯이

입니다. 이제 $\phi^{\pi}(s,a)$를 구해봅시다. 먼저 $\pi(a;s,\theta) \propto exp(\theta^{T}\phi_{sa})$ 이므로,
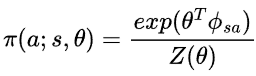
로 표현 가능하며, 정규화 항인 Z를 구해보면,

따라서,
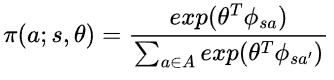
입니다. 이제 $\phi^{\pi}(s,a)$를 구해보면,
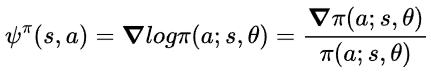
이므로,
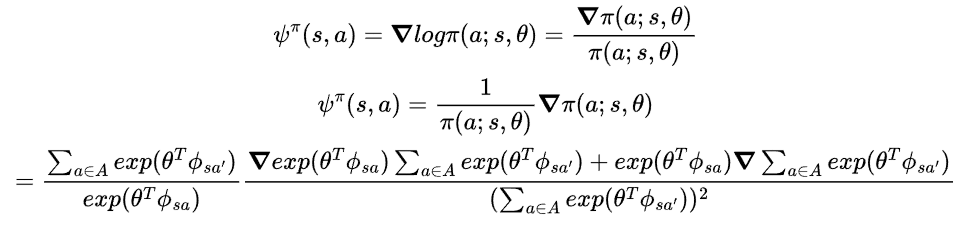
식을 전개하여 정리하면 최종적으로 다음을 얻습니다.

그런데, $E[\phi_{sa^{'}}]$는 $a$에 대한 함수가 아니기 때문에 결국 다음과 같은 식을 얻을 수 있습니다.

그리고 natural gradient step 이후 정책의 변화는 $\pi(a;s,\theta^{'}+\alpha\widetilde{\nabla}\eta(\theta)) \propto exp(\theta^{T}\phi_{sa}+\alpha\widetilde{\nabla}\eta(\theta)^{T}\phi_{sa})$ 가 됩니다. 여기서 gradient step이 매우 크다면, 즉 $\alpha \to \infty $라면, $\alpha\widetilde{\nabla}\eta(\theta)^{T}\phi_{sa}$의 영향력이 매우 커지기 때문에 이 gradient를 최대로 하는 행동의 확률은 1로 수렴하게 됩니다. 반대로 말하면, $a\notin argmax_{a^{'}}\widetilde{\nabla }\eta(\theta)^{T}\phi_{sa^{'}}$인 $a$에 대해서 $\pi_{\infty}(a,s)$는 $0$으로 수렴합니다.
Q.E.D.
이어서 다음 정리를 보겠습니다.
$Theorem 3.$ $\widetilde{\omega}$가 근사 에러를 최소화 시키는 값이고 파라미터의 업데이트를 $\theta^{'}=\theta+\alpha\widetilde{\nabla }\eta(\theta)$라고 한다면,

를 만족한다.
$Proof$
파라미터의 변화 $\Delta\theta$는 $\alpha\widetilde{\nabla }\eta(\theta)$이기 때문에, Theorem 1.에 의해 $\Delta\theta=\alpha\widetilde{\omega}$입니다, 따라서 정책의 변화량을 테일러 급수의 1차항으로 표현한다면 다음과 같습니다.

Q.E.D.
greedy action을 취하는 것은 항상 정책을 향상 시키는 것이 아닙니다. 그러나 line search 기법을 이용한다면, greedy action을 취함으로써 one step 향상을 보장할 수 있습니다. 또 피셔 정보 행렬은 positive definite이기 때문에 초기 향상이 보장됩니다.
5. Metrics and Curvatures
지금까지 우리는 피셔 정보 행렬 $F$를 도로 사용하였습니다. 그런데 다른 행렬을 척도로 사용할 수는 없을까요? 다양한 파라미터 추정에 있어서 피셔 정보 행렬은 Hessian에 수렴합니다. 그래서 피셔 정보 행렬은 Cramer-Rao 하한을 가지며 점근적으로 효율적입니다. 위키피디아를 보면 Cramer-Rao 하한은 확률적으로 분포하는 데이터의 분산에 대한 이론적인 하한이라고 합니다. 여기서 정의되는 하한은 피셔 정보의 역수가 됩니다.
Kakade는 이러한 상황이 파라미터 공간에 따라 척도를 정해야하는 blind source separation case와 비슷하다고 말합니다. 그리고 척도가 굳이 점근적으로 효율적일 필요가 없다고 합니다. Mackay는 Hessian에서 데이터 의존적인 항들을 척도로 쓰는 것이 하나의 전략이 될 수 있다고 주장했습니다.
피셔 정보 행렬은 좋은 선택이지만 Hessian($\nabla ^{2}\eta(\theta)$)과 어떤 관련이 있는지 좀 더 알아봅시다. Hessian은 다음과 같은 식으로 표현이 가능합니다.

불행히도 Hessian의 모든 항들은 데이터 의존적입니다.(Q함수의 존재 때문입니다.) 그렇기에 $\nabla Q^{\pi}$ 에 의존하는 나머지 두항에서 피셔 정보 행렬은 아무런 정보도 얻지 못합니다. 그리고 첫 번째 행렬은 $\nabla ^{2}\pi$ 때문에 피셔 정보 행렬과 관련이 있어 보입니다. 그러나 Q value가 미치는 영향을 피셔 정보 행렬은 무시합니다.
물론 우리의 척도가 Hessian으로 수렴할 필요는 없습니다. 또한 종종 Hessian은 postive difinite가 아니므로 Hesiian이 만들어내는 곡률은 파라미터가 local 극값에 가깝지 않다면 효용이 없을 수도 있습니다. 따라서 Congugate method가 극값 근처에서는 더욱 효율적일 수도 있습니다.
이번 장에서는 Kakade가 어떠한 논리로 글을 전개하였는지 디테일을 알기가 어려웠습니다. 다만 피셔 정보 행렬이 나타내는 곡률과 Hessian간의 관계를 더욱 알고 싶으신 분이라면
Martens, James. "New insights and perspectives on the natural gradient method." arXiv preprint arXiv:1412.1193 (2014)
paper가 큰 도움이 될 수 있을 겁니다.
6. Experiments
Kakade는 간단한 MDP부터 테트리스처럼 복잡한 MDP에서 natural gradient의 퍼포먼스를 실험하였습니다. 먼저 피셔 정보 행렬을 구해야하는데, 피셔 정보 행렬은 하나의 trajectory에 대하여 평균을 내어 구합니다. 즉,
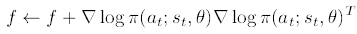
방식으로 $f$를 구한 다음 trajectory의 길이 $T$로 나누어 평균을 냅니다. 따라서 피셔 정보 행렬 $F$는 $f/T$로 추정합니다.
첫 번째로 실험한 MDP는 1차원의 Linear Quadratic Regulator(LQR)문제입니다. 이 LQR은 시그널u로 컨트롤하여 x를 0에 가깝게 만드는 것이 목표입니다. 동역학은 다음과 같습니다.
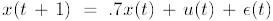
정책은 다음처럼 파라미터화된 정책을 사용하였습니다.
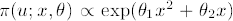
실험 결과는 아래 그림과 같습니다.

가장 오른쪽의 3가지 cost 곡선이 일반적인 gradient method를 사용했을 때 얻어진 곡선이고, 나머지 왼쪽 3개의 곡선은 natural gradient method를 이용하였을 때 얻은 곡선입니다. 실험 결과를 보면 역시나 natural gradient method를 사용했을 때가 더 좋은 퍼포먼스를 보여줌을 확인할 수 있습니다. 이 6개의 곡선은 서로 다른 파라미터 스케일로 사용된 정책을 이용하였습니다.
우리가 배운 natural gradient method는 정책 분포상에서 움직이기에 파라미터 공간에서 covariant 벡터입니다. 그런데 어째서 다른 스케일의 파라미터 공간에서 왜 다른 곡선을 보여주고 있을까요? (다시 말하면 covariant하지 않을까요?) 그 이유는 피셔 정보 행렬을 계산할 때 어쩔 수 없이 분포에 대한 확률 $\rho_{s}$를 가중치로 사용하여 계산하기 때문입니다. 따라서 이 문제를 풀기 위해 사용하는 natural gradient는 $\rho_{s}$에 의존하게 되며 따라서 진정한 covariant 벡터가 아닙니다.
$\rho_{s}$에 대한 영향은 두 번째 실험에서 확실히 드러납니다. 두 번째 실험은 다음과 같습니다.
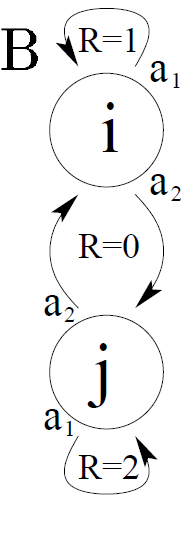
위 그림에서 i 노드에서 self-loop를 선택할 행동의 확률을 계속 증가시킨다면 j 노드에서 머물 시간이 줄어들것입니다. 다시 말하면, 이러한 행위는 j에서의 stationary probability를 줄게 할것입니다. 정책 근사로 시그모이드형의 함수를 사용하고 초기 상태를 $\rho(i)=.8\ \ and\ \ \rho(j)=.2$라고 하겠습니다. 이제 gradient를 통한 학습을 진행하면 각 노드에서는 self-loop를 선택할 확률이 초기에는 늘어날 것입니다. (왜냐하면 one-step 정책 향상은 각 노드에서 self-loop를 선택할 것이기 때문입니다.)
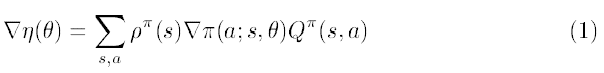
일반적인 gradient는 위의 식 (1) 처럼 각 학습에 stationary probability를 가중해주므로 self-loop 행위는 초기에 노드 i에서 노드j보다 더 많이 일어날 것입니다. 이렇게 되면 이 문제의 최적의 해 (노드j에서 계속 self-loop 행위를 선택하는 것)와는 다른 양상이 일어날 것입니다. 따라서 아래 그림처럼 리워드가 1인 극단적으로 평평한 구간이 나타나게 됩니다.

위의 그래프는 일반적인 gradient를 사용했을 때의 결과입니다. 무려 1500000 time이 흘러도 리워드는 1인 것을 확인할 수 있습니다. 반면 아래 그림의 점선 곡선은 natural gradient를 사용했을 때의 결과입니다. 시간이 겨우 2 time일 때 벌써 리워드는 1을 넘어가는 것을 확인할 수 있습니다. 그런데 natural gradient를 사용했을 때 초반에는 일반적인 gradient보다 리워드가 작습니다. 그 이유는 일반적인 gradient는 노드 i에 붙어있으려고 하기 때문입니다.
각 학습이 진행되고 있을 때 실제로 파라미터 $\theta$는 어떤 거동을 보일까요? 아래는 일반적인 gradient를 사용 했을 때(실선)와 natural gradient를 사용했을 때(점선)을 비교한 그림입니다.

natural gradient(점선)을 사용했을 때 훨씬 파라미터들이 균등하게 학습이 되고 있음을 확인할 수 있습니다.
이제 보다 복잡한 MDP인 테트리스에 대한 실험 결과를 보겠습니다.
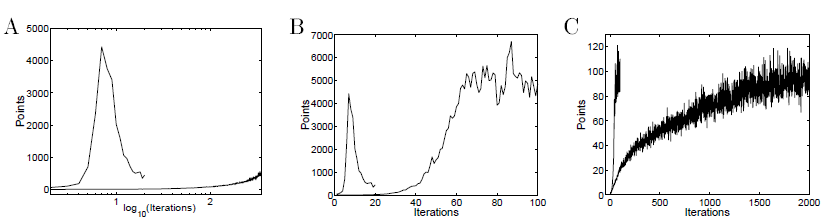
가장 먼저 그림 A는 두 가지 곡선을 보여줍니다. 위로 솟았다가 다시 내려온 곡선은 greedy policy iteration방법을 이용했을 때의 거동입니다.(단 선형 근사 함수를 사용하였음.) 그리고 그 밑에 아주 천천히 상승하고 있는 곡선은 일반적인 gradient 방법을 사용한 policy gradient method 방법을 이용했을 때의 모습입니다. 재밌는 점은 policy iteration을 사용했을 때 gradient method 방법을 사용했을 때보다 훨씬 빠르게 학습이 되었지만 갑자기 급격하게 떨어지는 모습을 볼 수 있습니다. 왜 그런지는 설명할 수는 없지만요.
그림 B는 natural gradient method를 이용하였을 때의 모습을 보여줍니다. 이 곡선의 모습은 natural gradient는 greedy policy 향상의 방향으로 움직이고 있다는 4장의 이론과 일치합니다. natural gradient method는 처음에는 greedy policy iteration보다는 느립니다. 그 이유는 매 step을 더 작게 설정하였기 때문입니다. 그러나 greedy policy iteration과는 달리 성능의 급격한 감소가 나타나지 않습니다.
그리고 마지막 그림 C에서는 natural gradient method(왼쪽)과 일반적인 gradient method 방법을 사용했을 때의 거동을 비교하였습니다. natural gradient method가 초기에는 훨씬 빠르게 수렴하지만 최종적으로는 결국 같은 지점에 수렴함을 확인할 수 있습니다.
7. Discussion
이 장에서는 Kakade는 natural gradient method가 greedy optimal action을 취하도록 학습이 된다는 점을 강조하고 있습니다.
gradient methods가 greedy policy iteration 방법처럼 정책을 크게 변화시키지는 못하더라도 4장에서 확인하였듯이 이 둘은 유사성을 가지고 있습니다. 왜냐하면 natural gradient method는 항상 정책 향상의 방향으로 움직이기 때문입니다. 더 나아가 line search 기법을 사용한다면 이 두 방법은 더 비슷해질 수 있습니다. 더욱이 natural gradient method는 성능 향상이 보장되어있습니다. 하지만 파라미터 공간에서 극값과 가까운 부분에서 natural gradient는 아주 작은 gradient 값을 가지기에 conjugate method가 더 빨리 수렴할 수도 있습니다. 이와 같은 모호성 때문에 Kakade는 natural gradient를 더 잘 이해하기 위해서는 추가적인 연구가 필요하다고 주장하며 끝을 맺습니다.
리뷰를 마치며
처음에 natural gradient는 단순히 2차 미분을 이용한 테크닉이라고 생각했던 저를 반성하는 시간이었습니다. 직교하는 파라미터 공간에서 구현되는 휘어진 분포 공간. 그리고 이 휘어진 공간을 파헤치기 위해 상대성 이론에 주로 등장하는 covariant 벡터의 개념까지…
특히 피셔 정보 행렬이 두 분포의 KL divergence의 Hessian과 같다는 사실이 매우 놀라웠습니다. 더 나아가 compatible function approximation과 같은 중요하고 fundamental한 기본 지식을 습득할 수 있는 계기가 되었습니다.
사실 TRPO를 리뷰하기 위해 본 논문이지만 상당히 많은 내용을 얻어갈 수 있었습니다. 더불어 Kakade와 같은 대가들을 보며 많은 부족함을 느끼며 공부에 동기 부여를 받는 시간이었습니다.
더 나아가 강화학습의 관점에서 Natural Policy Gradient에 더 알아보고 싶으신 분이라면 아래의 논문을 추천드립니다.
[Provable Global Convergence of Natural Policy Gradient, 2019]
'Paper Review' 카테고리의 다른 글
| Planning with Goal-Conditioned Policies (2019) 논문 리뷰 (2) | 2023.05.14 |
|---|---|
| Reference Learning and Control as Probabilistic Inference: Tutorial and Review 논문 리뷰 (0) | 2022.06.12 |
| Variational Adversarial Imitation Learning (VAIL) 논문리뷰 (0) | 2022.02.26 |
| Trust Region Policy Optimization 논문 리뷰 (1) | 2022.02.22 |
| Generative Adversarial Imitation Learning (GAIL) 논문리뷰 (4) | 2021.12.29 |



