리뷰 작성: 김한결 / 석사과정 (gksruf621@postech.ac.kr)
<Imitation learning 목차를 읽고 와주세요!>
0. Preliminary
GAIL의 내용을 두문장으로 요약하자면 다음과 같습니다.
1. apprenticeship learning via inverse reinforcement learning(APP), Maximum Entropy Inverse Reinforcement Learning(MaxEntIRL) 등 기존의 IRL 알고리듬을 occupancy measure matching을 이용하여 일반화 할 수 있으며 IRL과 RL을 동시에 수행할 수 있다.
2. occupancy measure matching식에서 특수한 Regularizer를 사용함으로써 GAN과 유사한 형태의 RLㅇIRL 알고리듬을 제시한다.
이제 1번에 관련된 이야기를 시작하겠습니다.
GAIL의 수식(1)번은 MaxEntIRL의 최적화 문제입니다.

그런데 위 수식을 MaxEntIRL 논문에서 찾을수가 없기 때문에 위 수식을 보고 당황하시는 분이 몇몇 있으실 겁니다. 대신 아래와 같은 수식이 있는데, 위와 아래 수식이 같다는 것을 증명해보겠습니다.

$P(\tau|\theta) = {1 \over Z}e^{r(\tau)} \rightarrow \underset{\theta}{argmax}\underset{examples}{\Sigma}\log{P(\tilde{\tau}|\theta)} = \underset{\theta}{argmax}\underset{examples}{\Sigma}\log{{e^{r(\tilde{\tau})}} \over \int e^{r(\tau|\theta)} d\tau}$
$=\underset{\theta}{\max}{1 \over N}\underset{\tau\in exam}{\Sigma}r(\tilde{\tau})-\log{Z}, where \, Z\,is \int e^{r(\tau|\theta)} d\tau$
$Z$만 조금 변형하겠습니다.
$ Z = \int q(\tau){e^{r(\tau|\theta)} \over q(\tau)}d\tau \overset{approx}{\rightarrow} {1 \over M}\underset{D \in sample}{\Sigma}{e^{r(\tau_i|\theta)} \over q(\tau_i)}$
여기서 q는 $\tau$에 관한 어떠한 함수여도 상관이 없습니다. 그러나 저희는 샘플링 가능한 분포를 사용할 겁니다. 자세한 내용은 조금 더 밑에 있습니다.
여기서 $logZ$는 아래와 같으며, 우리는 $\theta$로 편미분을 한번 해줘봅시다.
$logZ = log{1 \over M}\underset{\tau_j\in D_{sample}}{\Sigma}{{e^{r(\tau_j|\theta)}} \over q(\tau_j)}$
$\nabla_\theta logZ={1 \over Z}{\partial Z \over \partial \theta} = {1 \over Z}{1 \over M}\underset{\tau_j\in D_{sample}}{\Sigma}{{e^{r(\tau_j|\theta)}} \over q(\tau_j)}{\partial r(\tau_j|\theta) \over \partial \theta}$
시그마 앞 $Z$를 안으로 넣어주면
$={1 \over M}\Sigma{{e^{r(\tau_j|\theta)}} \over Z}{1 \over q(\tau_j)}{\partial r(\tau_j|\theta) \over \partial \theta}$
$P(\tau|\theta) = {1 \over Z}e^{r(\tau)}$ 이므로
$={1 \over M}\Sigma{\partial r(\tau_j|\theta) \over \partial \theta}$ $=\int q(\tau_j){\partial r(\tau_j|\theta) \over \partial \theta}$
잠시 다른식을 $\theta$로 미분한 결과를 살펴봅시다.
$\nabla_\theta\int q(\tau_j)log({{e^{r(\tau_j|\theta)}} \over q(\tau_j)}) =\nabla_\theta\int q(\tau_j)log({e^{r(\tau_j|\theta)}})$
$=\nabla_\theta\int q(\tau_j)r(\tau_j|\theta) = \int q(\tau_j){\partial r(\tau_j|\theta) \over \partial \theta}$
위 식이 $logZ$를 $\theta$로 편미분한 것과 같으므로 대체할 수 있습니다. 그런데 잠시 위에서도 sampling 기법을 이용해 근사하였으므로 여기서도 근사해서 대입하도록 합시다.
$\int q(\tau_j)log({{e^{r(\tau_j|\theta)}} \over q(\tau_j)}) \approx {1 \over M}{\Sigma}r(\tau_i) - {1 \over M}\Sigma\log{q(\tau_i)}$
위를 저희가 풀던 식에 대입하면 아래와 같습니다.
$\rightarrow \underset{\theta}{\max}{1 \over N}\underset{examples}{\Sigma}r(\tilde{\tau})-{1 \over M}{\Sigma}r(\tau_i)+{1 \over M}\Sigma\log{q(\tau_i)}$
앞서 q가 샘플링 가능한 어떠한 함수여도 상관이 없다고 하였는데, 저희가 샘플링할 수 있는 $\tau$에 관한 분포는 오직 하나밖에 없습니다. 바로 $\pi(\tau)$입니다. 또한 trajectory인 $\tau$를 s와 a로 쪼개어 아래처럼 쓸 수 있습니다.
$=\underset{\theta}{\max}\mathbb{E}_{\pi_{E}}[r(s,a)]-\mathbb{E}_{\pi}[r(s,a)]-\mathit{H}(\pi)$
r(s,a)을 -c(s,a)로 변경하고, 위 식은 IRL 부분만을 담고 있으니 $\pi^*$를 찾는 RL 부분도 함께 써주면 다음과 같은 식이 완성됩니다.
$=\underset{\theta}{\max}-\mathbb{E}_{\pi_{E}}[c(s,a)]+\underset{\pi}{min}(\mathbb{E}_{\pi}[c(s,a)]-\mathit{H}(\pi))$
이로써 MaxEntIRL의 최적화 문제가 GAIL의 수식(1)과 동일하다는 것을 증명했습니다.
(위 증명과정은 Finn 교수님의 영상[1]과 A Connection Between...논문[2], Guide Cost...논문[3]을 참고하여 제가 유도한 것이기 때문에 증명이 잘못되었을 수 있습니다. 혹시 잘못된 점을 발견하시면 말씀해주세요. )
1. Motivation
저희 블로그 - Imitation learning에서 언급했던 3가지 논문을 읽으셨다면, 위 최적화에는 문제점이 있다는 것을 알 수 있습니다. IRL과 RL을 각각 따로 여러번 수행해야 하기에 large environment에 적합하지 않기 때문입니다. GAIL논문은 이러한 문제를 해결하기위해 IRL과 RL을 동시에 하고싶다는 동기에서부터 시작됩니다.
2. occupancy measure matching과 RLㅇIRL 증명
지금부터는 논문 page 2~3부분의 Proposition, Lemma, Corollary를 차근차근 하나씩 볼 예정입니다.
그전에 잠시 2가지 내용을 미리 숙지하셔야합니다. 첫번째로는 MaxEntIRL식을 일반화하기위해 GAIL의 식(3)과 같이 Regularizer를 추가해줍니다. 이때 $\psi$는 convex하다고 합시다.(Regularizer를 추가하는 것이 왜 일반화되는 것인지는 section3에서 설명 합니다)
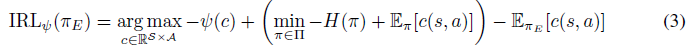
두번째로는 convex conjugate가 Proposition 3.2에서 필요하니 정의를 살펴보겠습니다. 논문에는 아래와 같이 적혀 있고 논문을 읽고도 이해가 안가신다면 몇몇 분들이 포스팅한 내용을 참고하시면 될 것 같습니다. 여기서는 convex conjugate function이 항상 convex하다는 점만 알아두시면 됩니다.

이제 본격적으로 Proposition, Lemma, Corollary를 살펴봅시다.
첫 목표는 RL과 IRL을 동시에 할 수 있다는 것을 의미하는 Proposition 3.2를 증명하는 것입니다.

이를 위해 가장 먼저 봐야할 부분은 Proposition 3.1과 Lemma 3.1입니다. 이에대한 증명은 각각 refer[29]와 Appendix A.1(추가로 refer[6]의 page32-2.106을 보시면 됩니다)에 나와 있으니 읽어보시면 됩니다. 여기서 중요한 점은 $\pi_{\rho}$와 매칭되는 occupancy measure $\rho$는 유일하다는 것(Proposition 3.1)과 $\bar{\mathit{H}}$가 strictly concave라는 점(Lemma 3.1)입니다.


이제 Appendix A.1의 Proof of Proposition 3.2로 넘어가보겠습니다. 저희는 식(31,32 혹은 34)로 얻은 policy가 식(35,36)으로 얻은 policy가 같다는 것을 증명하면 됩니다.(여기서 식(35,36)으로 얻은 $\rho$는 GAIL의 식(3)으로 얻은 $\pi$와 동일합니다-Proposition 3.1)


최적화해야하는 함수 $\bar{\mathit{L}}(\rho,c)$를 다음과 같이 표현하겠습니다.

이때 $\rho$를 고정시킨 $\bar{\mathit{L}}(\centerdot,c)$는 $\psi$가 convex이기 때문에 concave이고 $c$를 고정시킨 $\bar{\mathit{L}}(\rho,\centerdot)$은 $\bar{\mathit{H}}$가 concave이기 때문에 convex입니다.(저도 여기서 조금 헷갈리는 부분이 $\underset{s,a}{\Sigma}\rho(s,a)c(s,a)$가 convexity에 영향을 줄 것 같은데, 해당 논문에서는 이 부분을 고려 안하는 이유가 무엇인지 의문입니다)
따라서 minmax duality 성질에 따라 식(37)이 성립합니다.
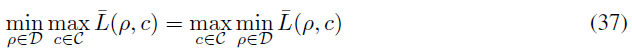
이를 조금 더 풀어서 설명하자면 식(35)에서 $\tilde{c}$를 찾을때 $\bar{\mathit{L}}(\rho,c)$을 최소화하는 $\rho$를 먼저 찾아야하지만 이러한 과정없이 c에 대해 $\bar{\mathit{L}}(\rho,c)$를 최대화하는 $\tilde{c}$를 찾아도 같은 $\tilde{c}$를 얻을 수 있다는 뜻입니다. 이렇게 얻은 $\tilde{c}$를 식(36)번에 대입하게 되면 정확히 식(34)와 같아지게 됩니다. 이로써 Proposition 3.2를 증명하였습니다.
이제 Corollary 3.2.1을 같이 살펴봅시다.(중요하지 않기때문에 넘어가셔도 됩니다.
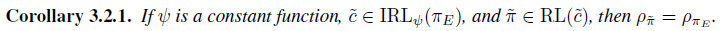
여기서 Corollary 3.2.1이 말하는 바는 regularizer를 constant로 두면, Proposition 3.2를 풀었을때 얻는 정책은 expert의 정책과 동일하다는 것입니다.

$\tilde{c}$를 찾는 식(6)을 2,3항을 $c(s,a)$로 묶는다면 $ \lambda = c(s,a)$인 어떤 primal문제의 dual problem으로 볼 수 있습니다.(convex optimization을 참고하세요) 여기서 $-\bar{\mathit{H}}$가 strictly convex이기 때문에 primal optimum과 dual optimum이 같고 $\tilde{\rho} = \underset{\rho \in D}{argmin}\bar{\mathit{L}}(\rho,\tilde{c}) = \underset{\rho \in D}{argmin}-\bar{\mathit{H}(\rho)}+\underset{s,a}{\Sigma}\tilde{c}(s,a)\rho(s,a) = \rho_{E}$가 성립합니다. 즉, expert의 policy와 완전히 동일할때 최적의 policy를 갖는다는 뜻입니다.(저는 위 식보다 primal문제의 optimal한 값이 유일하고 dual과 같기때문에 constraint를 지켜야하므로 $\rho=\rho_{E}$로 생각하는게 더 편했습니다)
마지막으로 Lemma 3.2는 저희가 지금까지 증명했던 사실을 이용하면 너무도 당연한 사실입니다.(Proposition 3.1 참고)
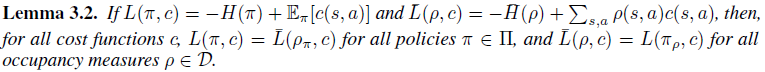
이것으로 page 2~3에 있는 Proposition, Lemma, Corollary를 전부 보았습니다.
이제 Practical한 approch를 봅시다.
3. Practical occupancy measure matching
전술한 바와 같이 $\rho=\rho_{E}$이면 최적입니다. 하지만 저희는 expert tracjectory finite하게 가지고 있기 때문에 environment의 state, action의 space가 large해질수록 많은 trajectory가 필요하며 이는 practical함과는 거리가 있게됩니다. 이를 위해 occupancy measure가 다른 정도를 smoothly penalize한 것이 식(8)입니다.

여기서 $d_{\psi}(\rho_{\pi},\rho_{\mathit{E}}) := \psi^*(\rho_{\pi}-\rho_{\mathit{E}})$입니다.
앞서 section2 초반부에 $\psi$라는 regularizer를 추가하는 것이 일반화하는 과정이라고 하였습니다. 그런데 Apperentice learning(Abbeel and Ng[1] and Syed et al.[29])의 수식을 보면 regularizer항이 없습니다.(식 (9) 참고) 그 대신 cost function을 representation하는 공간의 제약이 있죠.(Abbeel and Ng의 경우 linear, Syed et al는 convex)
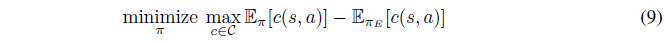
그렇다면 식(8)과 식(9)를 동일하게 만들어 주게끔 $\psi$가 cost function을 representation하는 공간을 제약하도록 잡아주면 되겠죠. 그러한 $\psi$가 아래 식의 $\delta_{c}$입니다.
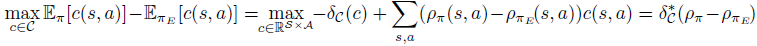
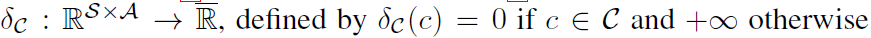
$\delta_{c}$ 정의상 cost function의 공간안에(예 : Abbeel and Ng의 경우 linear해야함) 있지 않으면 $-\infty$가 되기때문에 좌변과 같은 식이 됩니다. 여기서 Entropy항을 추가해주면 Entropy-regularized apprenticeship learning이 되며 (식 (11)) $-\mathit{H}(\pi)$항 또는 $\underset{c \in C}{\max}\mathbb{E}_{\pi}[c(s,a)]-\mathbb{E}_{\pi_{\mathit{E}}}[c(s,a)]$항에 $\alpha$ 곱하므로 entropy regularization strength를 조절할 수 있습니다.

그 다음으로 식(11)번 밑으로 기술되는 Entropy-regularized apprenticeship learning의 장단점을 간단히 살펴보면, 단점으로는 $\pi_{\mathit{E}}$이 $C$에 인코딩 되지 않을 수 있다는 점이 있고(C의 공간이 linear 혹은 convex이기 때문) 장점은 그럼에도 불구하고 approximation을 할 수 있기때문에 large state 와 large action 공간을 다룰 수 있다는 점입니다.
4. Generative adversrial imitation learning
드디어 preliminary에서 언급한 2번을 이야기할 차례가 왔습니다.
지금까지 RL과 IRL을 동시에 최적화 할 수 있다는 것과 해당 식을 regularizer를 도입함으로써 일반화를 살펴보았습니다. 그럼 어떤 regularizer를 사용해야 최적화하기 쉬우면서 $\pi_{\mathit{E}}$이 $C$에 인코딩되게 할 수 있을까요? 해당 논문에서는 아래와 같은 regularizer를 제안합니다.

식(13)을 사용하면 식(8)을 식(15)와 같은 최적화문제로 바꿀 수 있는데, 식(14)는 딥러닝하는 분들에게는 익숙한 GAN의 loss 형태입니다.

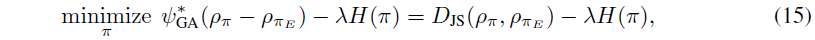
regularizer 위와 같이 정의한 목적을 조금 풀어서 말하자면, c의 공간을 넓힐 수 있으면서 저희에게 최적화하기도 쉬운 regularizer를 찾고 싶은데 식(13)과 같이 regularizer를 정의하면 두가지 모두를 만족할 수 있다는 것입니다.
그럼 식(13)의 conjugate function이 어떻게 식(14)와 같은지 잠시 살펴봅시다. 해당 내용은 Appendix의 A.2 proofs for section5에 있습니다.
우선 전체적인 큰그림을 말씀드리자면, minimum expected risk $R_{\phi}$가 $f$-divergence와 대응되며(refer [19]) jensen-Shannon divergence는 $f$-divergence의 특수한 case입니다. 저희는 $R_{\phi}$와 $\psi^*$가 같음을 보임으로써 식(13)의 conjugate function이 식(14)가 동일하다는 것을 증명할 것입니다.

우선 Prosition A.1을 봅시다.

위 그림에서 1번의 증명은 Proposition A.1 바로 밑에 있습니다.

(중요하진 않지만 참고로 여기서 $\phi$가 strictly decreasing convex이기때문에 $\phi^{-1}$도 convex입니다)
먼저 convexity를 살펴보면 $\phi$가 convex하기 때문에 $g_{\phi}$도 convex하고 $\rho_{\pi_{\mathit{E}}}(s,a)$의 정의를 잘 보면(논문 page 3에 있습니다) 각각의 $\rho_{\pi_{\mathit{E}}}(s,a)$를 어떤 상수로 생각할 수 있기 때문에 $\rho_{\pi_{\mathit{E}}}(s,a)g_{\phi}c(s,a)$도 convex하고 convex의 합은 convex이기 때문에 $\psi$도 convex합니다.
proper와 closed는 위 증명에서도 충분히 설명하고 있기때문에 넘어가도록 하겠습니다.
그 다음은 2번을 증명할 차례입니다. 아래 증명에 어려운 부분이 없기때문에 쭉 읽어보시면 됩니다. 그럼에도 이해하기 어려운 부분이 있다면 식 (43)에서 식 (44)로 넘어가는 부분일텐데, 식(40)에서 $c(s,a) \in \mathit{T}$이기 때문에 $-\phi$의 치역과 범위가 같아 변환이 가능합니다.

이렇게 Propostion A.1의 증명이 끝났습니다. 그 뒤로 이어지는 Corollary A.1.1는 Propostion A.1의 특수한 case를 설명하는 부분입니다. 여기서 특수한 case란 Propostion A.1의 $\phi(x) = \log{(1+e^{-x})}$인 경우를 의미합니다.
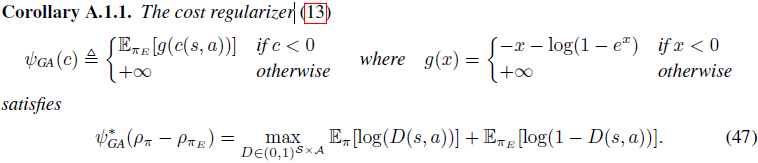
해당 부분의 증명은 그저 대입만 하면 되기 때문에 별다른 설명이 필요하지 않습니다.

Corollary A.1.1을 증명함으로써, 식(8)의 regularizer를 식(13)을 사용했을때 식(15)와 같음을 보였습니다.
5. GAIL Algorithm
GAIL 알고리듬은 다음과 같고 구현적인 관점에서 한 줄로 요약하자면 'GAN을 이용해서 expert로부터 생성되었는 감별하는 Discriminator를 학습하고 이를 이용해 얻을수있는 cost를 가지고 정책을 업데이트한다' 입니다.

알고리듬 table의 5번을 보시면 TRPO를 사용하고 PPO로 대체 가능합니다.(구현된 대부분의 코드들은 PPO를 사용하고 있습니다) 추가적으로 식(18)과 Lemma A.1에서 causal entropy graident와 관련된 내용이 적혀있지만 그렇게 중요한 부분은 아니니 넘어가도록 하겠습니다.
6. Experiments
실험은 Mujoco의 9개 task들로 진행 했으면 비교군으로는 다음 3가지 알고리듬을 사용하였습니다.
1) Behavioral clonning(BC) : expert의 70%는 학습 30%는 validation으로 사용. supervised.
2) Feature expectation matching(FEM) : Abbeel and Ng[1]가 제안한 $C_{linear}$방식으로 cost를 찾고, 정책 업데이트는 Ho et al.[11]을 사용.
3) Game-theoretic apprenticeship learning(GTAL) : Syed and Schapire[28]가 제안한 $C_{convex}$방식으로 cost를 찾고, 정책 업데이트는 Ho et al.[11]을 사용.
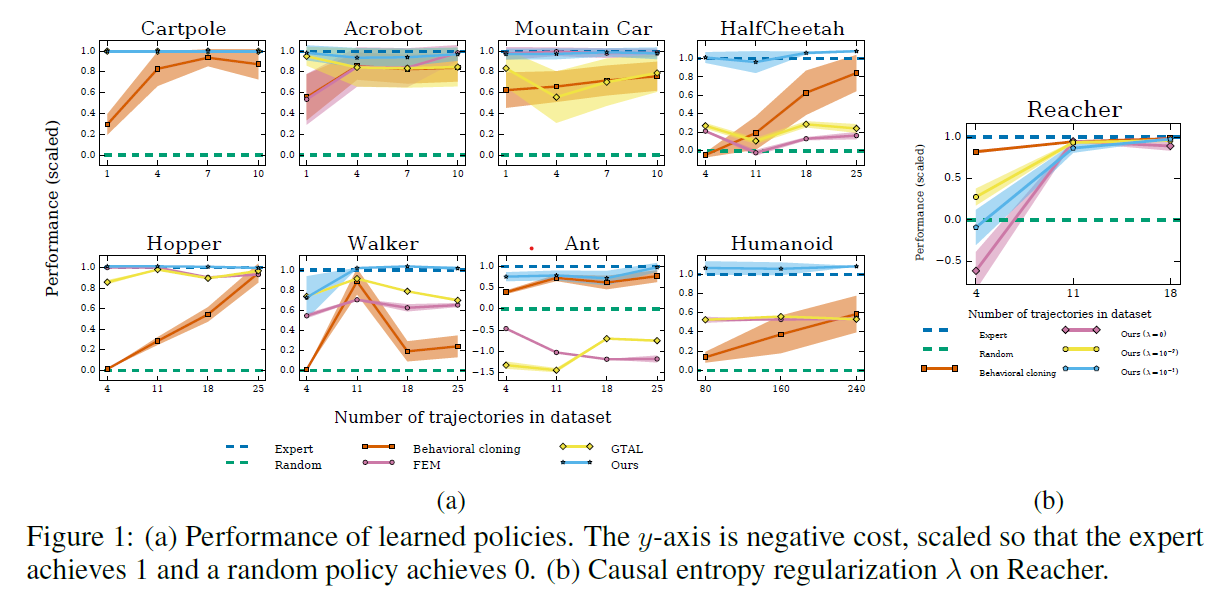
대부분의 task에서 다른 알고리듬에 비해 좋은 성능을 보여주었고, 모든 데이터셋 크기에 있어서 최소 expert의 70%이상의 성능을 보여주었습니다.
[1] https://www.youtube.com/watch?v=d9DlQSJQAoI
'Paper Review' 카테고리의 다른 글
| Planning with Goal-Conditioned Policies (2019) 논문 리뷰 (4) | 2023.05.14 |
|---|---|
| Reference Learning and Control as Probabilistic Inference: Tutorial and Review 논문 리뷰 (4) | 2022.06.12 |
| Variational Adversarial Imitation Learning (VAIL) 논문리뷰 (2) | 2022.02.26 |
| Trust Region Policy Optimization 논문 리뷰 (3) | 2022.02.22 |
| Natural Policy Gradient 논문 리뷰 (1) | 2022.02.14 |



